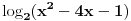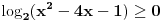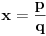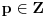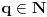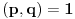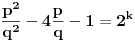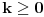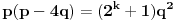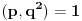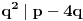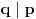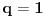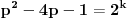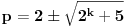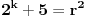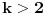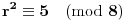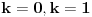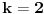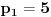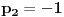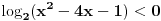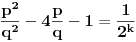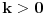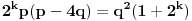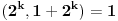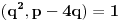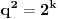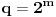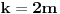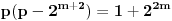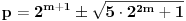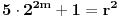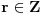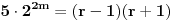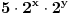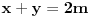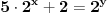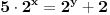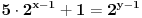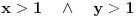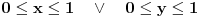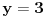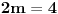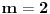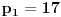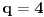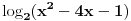
U zavisnosti od znaka izraza imaćemo dva slučaja.

1. slučaj:

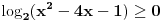
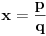
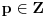
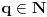
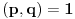
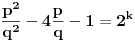
, , , tj. , za neko .

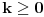
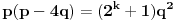
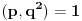
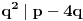
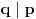
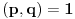
Iz i sledi a odatle pa zbog sledi .

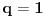
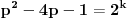
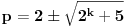
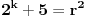
Dakle, imamo tj. pa mora biti za neko celo .

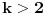
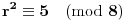
Ako je , onda je što je kontradikcija (jer kvadratni ostaci po modulu su samo i ).

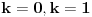
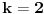
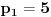
Proverom utvrđujemo da za nema a za ima rešenja, odakle imamo i .

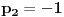
2. slučaj:

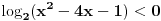
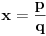
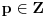
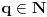
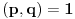
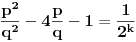
, , , tj. , za neko .

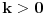
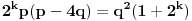
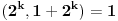
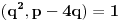
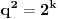
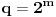
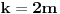
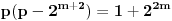
Iz , i sledi tj. za neko prirodno za koje je . Otuda imamo tj. .

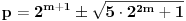
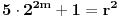
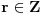
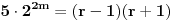
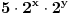
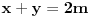
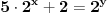
Ostaje da rešimo jednačinu , tj. . Jasno je da se desna strana može zapisati u obliku za neke nenegativne cele i takve da . Faktori na desnoj strani se razlikuju za pa je ili ili .

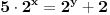
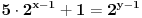
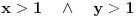
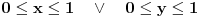
Prva mogućnost otpada jer deljenjem cele jednakosti sa dobijamo , pa bi u slučaju leva i desna strana bile različite parnosti. Jednostavnom proverom preostalih mogućnosti () vidi se da nema rešenja.

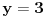
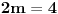
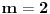
Sličnom analizom dolazimo do zaključka da drugi slučaj ima jedinstveno rešenje , a otuda i tj. tako da konačno imamo , , .

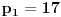
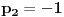
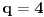
@d3x:

Drugi zadatak je izuzetno lak - razmisli još malo
Ako nije tajna možda bi mogao da nam kažeš odakle su ovi zadaci...

_{[Ovu poruku je menjao uranium dana 10.10.2006. u 09:30 GMT+1]}

Ovaj prvi zadatak je sa prve godine elektrotehničkog fakulteta u Sarajevu, zadaća 1 (prof. Huse Fatkic)
Imam neke informacije da ovaj zadatak koji sam isto poslao (to je sa proslogodišnje zadace) nije uradilo 90 posto brucosha, nekih 200 ljudi.

http://www.elitesecurity.org/t219867-sqrt

A stvarno po rjesenju mi se cini da je na jaaako visokom nivou u odnosu na nivo prve godine studija...

Kod ovakvih zadataka lako se može desiti da čovek previdi neku prečicu, dakle ne mora da znači da su data rešenja najjednostavnija. Meni se čini da je nivo zadataka elementaran, mada... možda zaista nije fer dati brucošima zadatak iz teorije brojeva jer verovatno većina srednjoškolskih programa mat. ne obraća dovoljno pažnje na tu oblast...