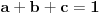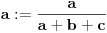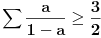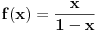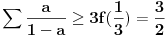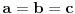[ iggy91 @ 15.10.2006. 07:14 ] @
| Za realne pozitivne brojeve a,b, i c dokazati da vazi nejednakost: a/(b+c) + b/(c+a) + c/(a+b) >= 3/2 ----------------------------------------------- Po mom misljenju zadatak treba raditi preko nejednakosti aritmeticke, geometrijske, kvadratne i harmonijske sredine. jedini problem je da ne znam koje 2 da kombinujem u prvom slucaju, a koje dve u drugom. Moze li pomoc? P.S. Hn - Harmonijska sredina Gn - Geometrijska sredina An - Aritmeticka sredina Kn - Kvadratna sredina Hn <= Gn <= An <= Kn Hn = n / (1/a1 +1/a2 +1/a3 + ... +1/an) Gn = n-ti koren(a1*a2*a3...*an) An = (a1+a2+a3+...+an) / n Kn = sqrt ( ( sqr(a1) + sqr(a2) + sqr(a3) + .... + sqr(an) ) / n ) |