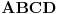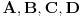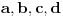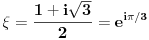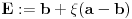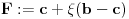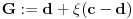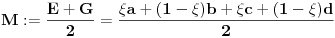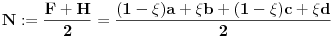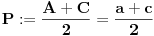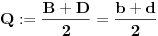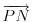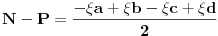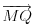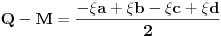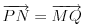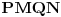[ pjervg @ 16.10.2006. 10:40 ] @
| Resavao sam ovaj zadatak i malo sam se zavrteo. Moze li pomoc? Zadatak: Nad stranicama konveksnog cetvorougla ABCD sa spoljasnje strane su konstruisani jednakostranicni trouglovi ABE, BCF, CDG i ADH. Ako su M,N,P,Q redom sredista duzi EG, HF, AC, BD dokazati da je cetvorougao PMQN paralelogram. |