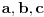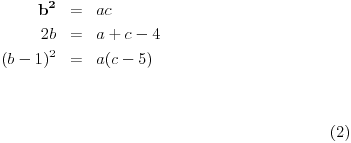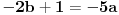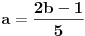Zadatak iz geometrijskog niza

[ maximus_1 @ 24.10.2006. 13:05 ] @

Tri su broja uzastopni članovi geometrijskog niza. Ako od trećeg oduzmemo 4, dobijemo tri uzstopna člana aritmetičkog niza. Ako zatim od drugog i trećeg oduzmmemo 1, opet dobijemo tri uzastopna člana geometrijskog niza. Koji su to brojevi?

Znači, imamo:

a_n+a_n+1+a_n+2 -> geometrijski niz,
a_n+a_n+1+a_n+2-4 -> aritmetički niz
a_n+a_n+1-1+a_n+2-5 -> geometrijski niz

E sad ne znam kako to iskoristiti da bi se dobili brojevi?

[ Farenhajt @ 24.10.2006. 14:21 ] @

Neka su brojevi

. Tada:

Iz treće jednačine je

(zbog prve), što daje

. Sada se to uvrsti u drugu da se dobije

preko

, a onda se izrazi za

uvrste u prvu da se dobije kvadratna jednačina po

[ Bojan Basic @ 24.10.2006. 14:34 ] @

Citat:

maximus_1:
Ako zatim od drugog i trećeg oduzmmemo 1, opet dobijemo tri uzastopna člana geometrijskog niza.
...
a_n+a_n+1-1+a_n+2-5 -> geometrijski niz

Kako tačno glasi postavka? I čemu služe oni plusevi u jednačinama — nisi li mogao da staviš, recimo, zareze?

Svejedno, Farenhajt ti je već rekao postupak, kako god da glase brojevi uradi na njegov način i dobićeš rešenje.

[ maximus_1 @ 24.10.2006. 19:45 ] @

Da, to je moja greška. Trebaju biti zarezi. Hvala

[ Bojan Basic @ 24.10.2006. 20:11 ] @

Dobro, pusti sad zareze, oduzima li se od trećeg broja 1 (kao što si napisao u tekstu) ili 5 (kao što si napisao u jednačini)? :)

[ Farenhajt @ 24.10.2006. 21:29 ] @

Bojane, u tekstu piše "ako ZATIM od drugog i TREĆEG oduzmemo jedan", što je saglasno s peticom u jednačini

Pride, s peticom se dobiju lepi racionalni brojevi, dok se s jedinicom dobije neko ne baš tako lepo korenje. Pretpostavljam da su autori problema ipak išli na naš mili em dragi skup Ku

_{[Ovu poruku je menjao Farenhajt dana 24.10.2006. u 22:49 GMT+1]}