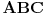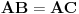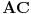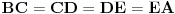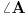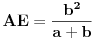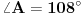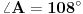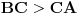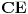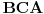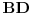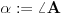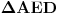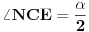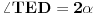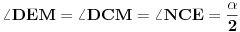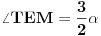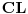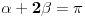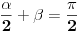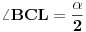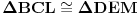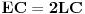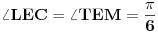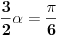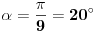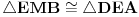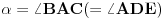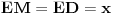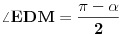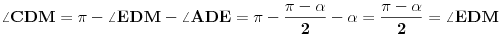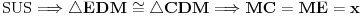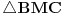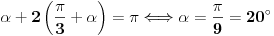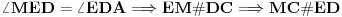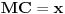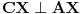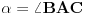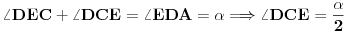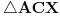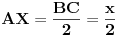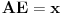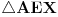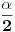[ Farenhajt @ 27.10.2006. 16:14 ] @
|
[ qzqzqz @ 27.10.2006. 17:27 ] @
[ Farenhajt @ 27.10.2006. 21:27 ] @
[ uranium @ 28.10.2006. 01:08 ] @
[ Farenhajt @ 28.10.2006. 01:54 ] @
[ uranium @ 28.10.2006. 02:32 ] @
[ Farenhajt @ 28.10.2006. 02:53 ] @
[ qzqzqz @ 28.10.2006. 08:23 ] @
da, da u pravu si, omasio sam uglove.
[ Farenhajt @ 30.10.2006. 20:14 ] @
[ Bojan Basic @ 30.10.2006. 21:33 ] @
Možete li da kažete koje programe koristite za crtanje slika? Meni je nekako najzgodniji Cabri Geometry, ovo uraniumovo mi liči na The Geometer's Sketchpad, dok ne mogu da prepoznam Farenhajtov program.
[ Farenhajt @ 30.10.2006. 23:15 ] @
Ja koristim domaćih ruku delo - Win GCLC (downloadujmo domaće, obnovimo Srbiju) - uglavnom zato što je u fully functional verziji potpuno besplatan.
[Ovu poruku je menjao Farenhajt dana 31.10.2006. u 13:32 GMT+1] [ mickey6252 @ 30.10.2006. 23:49 ] @
Reci mi molim Te, ili pošalji link za dld. Probao sam da "izguglujem" ali sam dobio samo informaciju da je autor softvera nagrađen nekom nagradom. Mislim, svaka čast, ali ...
[ Farenhajt @ 31.10.2006. 00:28 ] @
Google("GCLC"), drugi link po redu: http://www.matf.bg.ac.yu/~janicic/gclc
[ uranium @ 31.10.2006. 03:48 ] @
@Farenhajt:
Zaista prelepo rešenje...iznenađenjima nikad kraja @Bojan Basic: Da, u pitanju je The Geometer's Sketchpad 4.07S. Pre toga, najduže sam se služio već pomenutim WinGCLC-om, a neko kratko vreme koristio sam i Cabri Geometry II Plus. WinGCLC je zanimljiv program, naročito za one koji se "lože" na Logiku i Programiranje In the long run, not as user-friendly as advertised Što se tiče Cabri Geometry II Plus, nije bilo nekih suštinskih problema, naprosto više mi se dopao Sketchpad-ov interfejs (i graf. prikaz konstrukcije)... @Farenhajt: U vezi sa onim hintom: Pošto ćeš u narednim danima verovatno biti češće na forumu od mene, a kako verujem, nisi jedini zainteresovan za alternativna rešenja 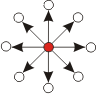 a možda je (u karmičkom smislu) poštenije da se prosleđuje žeton  [ Farenhajt @ 01.11.2006. 05:30 ] @
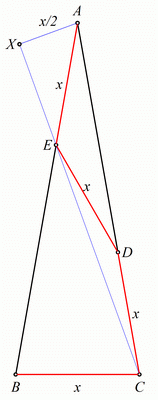
Maločas uočih još jedno rešenje, koje mi deluje najprostije dosad
[att_img] Uz 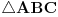 docrtajmo podudaran docrtajmo podudaran 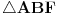 i na kraku i na kraku 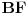 nađimo tačku nađimo tačku  takvu da je takvu da je 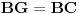 . Tada je po konstrukciji i početnim uslovima . Tada je po konstrukciji i početnim uslovima 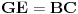 . Zatim . Zatim 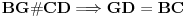 , pa je , pa je 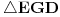 jednakostraničan, što daje jednakostraničan, što daje 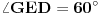 . S druge strane, očito je da je . S druge strane, očito je da je 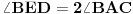 (spoljašnji ugao jednakokrakog (spoljašnji ugao jednakokrakog 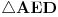 ) i da je ) i da je 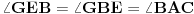 . Dakle, . Dakle, 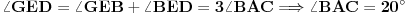 [Ovu poruku je menjao Farenhajt dana 01.11.2006. u 06:50 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|