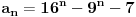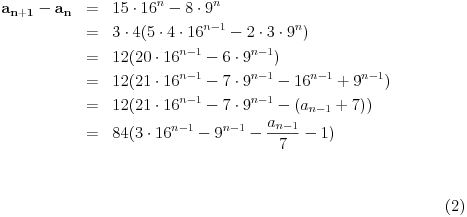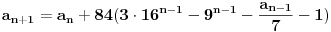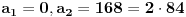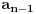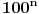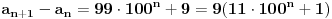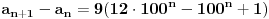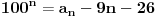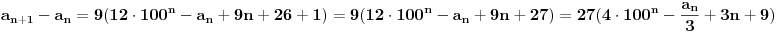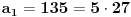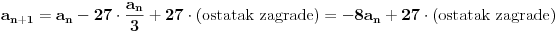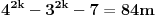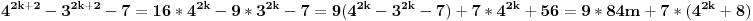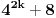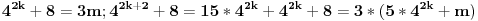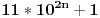Zadatak iz matematicke indukcije

[ Blejzer @ 07.11.2006. 07:57 ] @

Postovanje,

Imam dosta nekih zadataka koje ne mogu da rijesim, ali krenucu sa laksim:

84|4²ⁿ - 3²ⁿ - 7

potrebno je dokazati ovu tvrdnju putem matematicke indukcije.

Nakon razvijanja sa n=k+1
dobija se:

4^2k+2 - 3^2k+2 - 7 = 16*4^2k - 9*3^2k - 7 =

= e sad sta i kako dalje??? Pokusavao sam na razne nacine (dodavanjem i oduzimanjem,
kako bi dobio n*(4^2k-3^2k-7) + 'nesto' - sto bih dokazao da je djeljivo sa 84,
ali mi nikako ne ide... npr, dobijem 9(4^2k - 3^2k - 7) + 7*4^2k +7*8

Pozdrav

[ Farenhajt @ 07.11.2006. 15:41 ] @

Pa, prvo da pojednostavimo i stavimo

Tada je

Dakle,

. Sada je lako:

, a ako je

deljiv sa 84, onda je deljiv i sa 7.

[ Blejzer @ 08.11.2006. 01:43 ] @

Hvala velika. Izvanredno rjesenje!
Medjutim imam i dalje jedan problem, a to je sto mi i dalje nije jasno kako da ovaj princip napravim malo univerzalnijim...
slican zadatak, ali ne mogu da primjenim isti,slican ili drugaciji pristup... (ili bih mozda trebao ici malo odspavati???)

27|10²ⁿ + 9n + 26

Idem istim principom matematicke indukcije i dolazim do sledece tacke, gdje nekako gubim fokus...:

a_n+1 - a_n = 99*10²ⁿ + 9

Kako sad da izadjem iz ovog zacaranog kruga? 27 je 3³, 9 je 3² i sve imam osjecaj da su mi rjesenja pred nosom, ali ih ne vidim... Vjerovatno pad koncentracije...

Puno pozdrava,

[ Farenhajt @ 08.11.2006. 02:43 ] @

Prvo, otarasi se činilaca u eksponentu, tj. piši

.

Drugo, nisi daleko. Poenta je da "pakuješ" faktore tako da ispred zagrade dobiješ ono što ti treba, dakle 27. Prema tome

Sad bi nam dobro došla i jedna trojčica da je izvučemo iz zagrade, pa ćemo "napakovati" dvanaesticu od jedanaestice:

E sad je ključ: Ovaj

"viška" izraziš preko

, pa dobijaš

I tu je kraj, pošto je

, a ako je

deljiv sa 27, deljiv je i sa 3.

(A možeš izraz i malo srediti pa dobiti

, i pravolinijski imaš induktivni korak.)

_{[Ovu poruku je menjao Farenhajt dana 08.11.2006. u 03:55 GMT+1]}

[ blockyart @ 30.10.2008. 20:23 ] @

moze li milim te korak po korak obzirom da sam mrtvi pocetnik !
znacice mnogo u razvoju mojih vjestina iz math!
hvala hvala

[ h4su @ 31.10.2008. 11:27 ] @

Prvi mozes i ovako:

pretpostavka:

za k+1 imas

Sad treba dokazati da je

djeljivo sa 3 posto ocigledno djeljivo sa 4.

i gotovo.

Drugi kad dodjes do

treba pokazati da je

djeljivo sa 3,( ovaj broj je nesto oblika 110000001 zbir cifara mu je dljeljiv sa 3 pa je i on djeljiv sa 3 i to je to) a mozes da dokazujes da je ovo djeljivo sa 3 posebno kao i kod prvog zadatka.