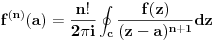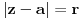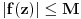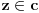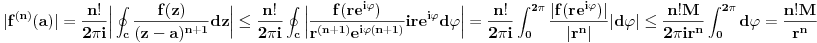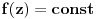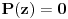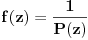Pa, ako znaš da svaki polinom P(z) stepena bar jedan sa kompleksnim koeficijentima ima barem jednu nulu (recimo w), onda istu teoremu možeš primeniti i na količnik P(z)/(z-w) i tako dobiti ostale nule.

Naravn da osnovni stav algebre moze da se dokaze preko Liouvillove teoreme, izvini sto se nisam ranije javio nisam vidio tread, nadam se da ce ovo da pomogne posto je tema stara 9 dana, a neko bi mogao da kaze ako postoji neka greska u dokazu...

Krenemo li od osnovne Kosijeve integralne teoreme :



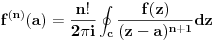
za n=0,1,2,3.... Treba prvo da dokazemo Cauchyevu nejednakost:

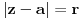
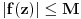
Ako je i za



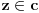
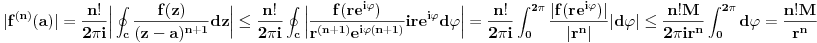
Iz prethodne nejednakosti za n=1 dobije se:

Sto tezi nuli kada r tezi beskonacnosti. Iz cega slijedi da je

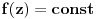
Teorema: Ako je funckija u prosirenoj kompleksnoj ravni regularna i ogranicena onda je ona konstanta.
Ovu teoremu je formulisao Liouville ali je prvi dokaz iznjeo Cauchy.

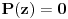
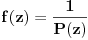
Ako jednacina nema korijena onda je funkcija regularna u cijeloj kompleksnoj ravni pa na osnovu gornje teoreme P(z) mora biti konstanta na cijeloj ravni sto naravno ne mora biti slucaj! Time je teorema dokazana.

_{[Ovu poruku je menjao bierkof dana 16.11.2006. u 22:10 GMT+1]}

Hvala.