Da li je posredi 1 radijan ili 1 stepen?

1 stepen

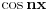
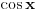
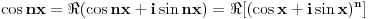
Pođi od Čebiševljevih polinoma prve vrste, koji kažu da se može izraziti kao polinom n-tog stepena s celobrojnim koeficijentima po argumentu (a to nije teško ni dokazati ako pođeš od , pa ovaj poslednji izraz razviješ po binomnom obrascu i izdvojiš realni deo)

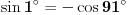
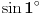
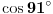
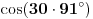
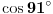
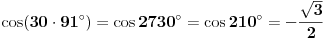
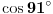
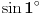
Sad imamo da je . Dakle, je racionalan ako i samo ako je racionalan . Pretpostavimo da je ovaj drugi broj racionalan. Tada će i broj biti racionalan, jer se može predstaviti kao polinom s celobrojnim koeficijentima od racionalnog argumenta . Međutim, . Dakle, ne može biti racionalan, te je i iracionalan.

hvala