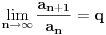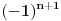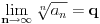U sustini mu dodje na isto.
Sustina je sledeca:
Kolicnicki kriterijum se koristi tako sto nadjes:
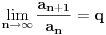
Pri cemu, ako je q<1, onda red konvergira, ako je q>1, red divergira, a ako je q=1, ne mozes na osnovu ovog kriterijuma da odredis konvergenciju reda (mozda si trebao da koristis korenski, posto je dosta precizniji ^_^)
E sad, ovo sve vazi samo pod uslovom da dobijes samo jedan rezultat pri nalazenju limesa, sto nije uvek slucaj. Ako npr dobijes neki red sa nezgodnim
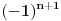
clanom, onda dobijes dva resenja, za n=2k i za n=2k+1. Tada treba da gledas lim inf, odnosno lim sup, sto ce reci, treba da gledas najmanje i najvece resenje. Ako je najmanje resenje vece od jedan, onda red divergira, a ako je najvece resenje manje od jedan, onda red konvergira.
Korenski kriterijum se koristi tako sto nadjes:
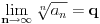
Pri cemu, ako je q<1, onda red konvergira, ako je q>1, red divergira, a ako je q=1, ne mozes na osnovu ovog kriterijuma da odredis konvergenciju reda.
Medjutim, ako dobijes vise resenja onda trazis lim sup, odnosno najvece i gledas da li je veci ili manji od jedan. Ako je veci, red divergira, ako je manji od jedan red konvergira.
______________________________________________________________________
Formalno gledano, ako dobijes samo jedno resenje limesa, to resenje je ujedno i supremum i infinum skupa resenja limesa. Tako da je preciznije definisati sve preko lim sup i lim inf. Na FTN-u, odsek elektrotehnika, na Matematickoj analizi 2, koristimo obican limes u definiciji, a lim sup i lim inf se navode kao specijalni slucajevi...
Kako ces ih definisati je formalizam, vazno je da razumes u potpunosti kako se koriste kriterijumi...