[ 069 @ 14.11.2006. 22:18 ] @
| Evo zadatka sa jednog drugog foruma: U pravouglom trouglu poznata je hipotenuza 15 cm i simetrala pravog ugla cija je duzina 5 cm.Konstruisati taj trougao. |
|
[ 069 @ 14.11.2006. 22:18 ] @
[ braker @ 15.11.2006. 01:29 ] @
Izvini,al' gde je tu problem?
[ Fuzz @ 15.11.2006. 12:49 ] @
Naizgled jednostavan, a ustvari potpuno infantilan :)
[ goky2002 @ 15.11.2006. 15:36 ] @
Ako nije problem, moze onda neko da postavi resenje ako ga ima
[ braker @ 15.11.2006. 20:49 ] @
Reshenje je ovde
Pogledaj deo:PRIMENE SLICHNOSTI NA PRAVOUGLI TROUGAO,a na slici ispod ovog naslova posmatraj stranicu b kao simetralu ugla,uzimajuci u obzir da je ugao ACD 45 stepeni,pa uz malo trigonometrije lako se dolazi do vrednosti Hc,pa zatim i p,a zatim i ugla CBA koji u ovom sluchaju zaklapa hipotenuza sa katetom.Sad kada su nam poznate velichine:kateta,hipotenuza i ugao lako se konstruishe trazheni trougao. Jel' to sa foruma neke osnovne shkole,il' je domaci [ Farenhajt @ 15.11.2006. 21:13 ] @
[ srki @ 16.11.2006. 06:14 ] @
Ne racunaju se uglovi nego npr. tangens ugla pa nema veze sto su takve vrednosti jer je taj tangens uvek moguce izraziti preko tih vrednosti koriscenjem mnozenja, delenja i korenovanja a onda je lako konstruisati taj ugao.
[ qzqzqz @ 16.11.2006. 07:31 ] @
[ Farenhajt @ 16.11.2006. 08:19 ] @
Sve je ovo kao kad bi se sa tri date stranice računao kosinus/tangens jednog unutrašnjeg ugla, pa onda trougao konstruisao preko SUS umesto direktno preko SSS. Batalite algebru, potražite čisto geometrijsku konstrukciju.
[ chupcko @ 16.11.2006. 10:14 ] @
Ja sam mozda blesav, ali ja nekako ne mogu da vidim one uglove o kojima vi pricate ????
Dakle ajde neko ko misli da je resio da podeli sa nama konstrukciju, ne mora dokaz :). [img]http://static.elitesecurity.org/uploads/1/3/1361184/a.svg[/img] ono sto znamo je sledece: ugao ACB je prav prava CD je simetrala ugla ACB duz AB je mere 15 duz CD je mere 5 [ Farenhajt @ 16.11.2006. 18:49 ] @
Evo recimo ovako može (priznajem da u konstrukciji ima malo algebre, tako da potraga za čisto geometrijskom konstrukcijom ostaje otvorena):
Na slici levo, neka je  presek simetrale i opisanog kruga. Tada je presek simetrale i opisanog kruga. Tada je 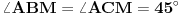 , pa je tačka , pa je tačka  jednoznačno određena kao središte polukruga s prečnikom jednoznačno određena kao središte polukruga s prečnikom  kome ne pripada tačka kome ne pripada tačka  , te je , te je 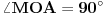 . .[att_img] Neka je 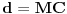 . Tada iz . Tada iz 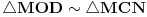 sledi sledi 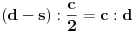 , što daje , što daje 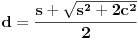 , pa se duž , pa se duž  može lako konstruisati kao što je prikazano na desnoj slici: može lako konstruisati kao što je prikazano na desnoj slici: 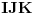 je ravnokrako-pravougli trougao s katetom je ravnokrako-pravougli trougao s katetom 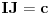 , kateta , kateta 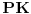 pravouglog trougla pravouglog trougla 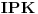 iznosi iznosi  , ,  je centar nacrtanog kruga, je centar nacrtanog kruga,  je središte duži je središte duži 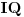 , , 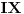 je jednako traženoj duži je jednako traženoj duži  . Na kraju iz tačke . Na kraju iz tačke  (na desnoj slici) opisujemo luk poluprečnika (na desnoj slici) opisujemo luk poluprečnika  do preseka s opisanim krugom, čime dobijamo treće teme traženog trougla. do preseka s opisanim krugom, čime dobijamo treće teme traženog trougla.Konstrukcija duži 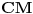 može se izvesti i na slici levo: Ako se spoje tačke može se izvesti i na slici levo: Ako se spoje tačke  i i  , pa se na duži , pa se na duži 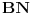 nađe tačka nađe tačka  takva da je takva da je 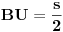 , pa se , pa se 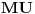 produži preko produži preko  do tačke do tačke  takve da je takve da je 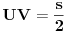 , onda je , onda je 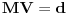 . .[ braker @ 16.11.2006. 20:50 ] @
@Farenhajt
Lepo,nisam ni sumnjao da cesh se uskoro pojaviti sa nekim konstruktivnim [ Farenhajt @ 16.11.2006. 21:33 ] @
I ja ću nastaviti potragu, a u međuvremenu, čisto radi potpunosti, da okačim i konstrukciju bez pomoćnih slika:
[att_img] Date su duži 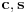 kojima su, zbog potreba konstrukcije, određena središta. Ostalo se vidi sa slike. kojima su, zbog potreba konstrukcije, određena središta. Ostalo se vidi sa slike.MODS: Da li još neko ima isti problem kao i ja, naime da mu ne izlazi samostalno slovo c u TeX-u? [ chupcko @ 17.11.2006. 08:57 ] @
[ 069 @ 17.11.2006. 16:41 ] @
Mozemo li da vidimo to "malo trigonometrije",Braker?Kako mislis da povezes ovu lekciju iz I razreda srednje skole sa simetralom pravog ugla?
Zadatak se moze resiti pomocu trigonometrije ali drugacije.Trazilo se konstruktivno resenje. Svaka cast,Farenhajt. [ Farenhajt @ 17.11.2006. 18:56 ] @
[ braker @ 17.11.2006. 20:39 ] @
Izvinjavam se shto nisam crtao slike uz objashnjenje,ali nemam trenutno niti jedan odgovorajuci program za tu namenu,pa cu se koristiti slikom sa linka iz prethodnog posta(mrzi me da instaliram
 je simetrala ugla je simetrala ugla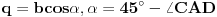 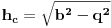 Iz slichnosti sledi da je: 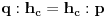 -odakle se dobija -odakle se dobija  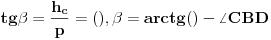 Napomena:tachka  je mesto preseka simetrale ugla i hipotenuze, je mesto preseka simetrale ugla i hipotenuze,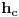 je normala spushtena iz je normala spushtena iz  na katetu. na katetu.Ako se ne varam,trigonometrija i homotetija i slichnost spadaju u program I r.s.sh. Citat: Trazilo se konstruktivno resenje. Konstruktivno reshenje je recimo i ono koje je postovao qzqzqz,jer mu je takav i pristup Citat: Zadatak se moze resiti pomocu trigonometrije ali drugacije. Da vidimo. [ 069 @ 20.11.2006. 10:25 ] @
Homotetija i slicnost su u I razredu, kvadratne jednacine u II a trigonometrija u I ili II(sa 4 i vise casova nedeljno u I razredu (samo na pravouglom trouglu) po vazecim programima u Srbiji).
[ 069 @ 20.11.2006. 11:08 ] @
Neka su p i q odsečci koje simetrala formira na hipotenuzi i neka je alfa ugao kod odsečka p a beta kod osečka q.Na osnovu zadatka i sinusne teoreme dobija se sistem:
p+q=15 alfa+beta=90 q/sin45=5/sin(beta) p/sin45=5/sin(alfa) Sve se to svede na sistem: alfa+beta=90 3*(2)^1/2=1/sin(alfa)+1/sin(beta) PS.I ja muku mucim sa pisanjem i posebno crtanjem slika.Kako vi resavate taj problem? [ 069 @ 20.11.2006. 11:12 ] @
Braker,kako dobijes q=bcos(alfa)?
[ braker @ 25.11.2006. 02:24 ] @
Ako je neko tragao za geometrijskom konstrukcijom,mozhda ce ga zanimati i odakle potiche zadatak
@069 Kako to da jedan diplomirani matematichar ne zna chemu je jednak kosinus nekog ugla? [ chupcko @ 25.11.2006. 14:59 ] @
Dakle definitno sam shvatio, ovaj zadatak je postavi neki palestinac koji kao ide u 6 razred onsovne skole. Mislim da je ovo jos jedan od onih zadataka koji su izgubljeni u prevodu :)))).
Tom uzrastu vise odgovara zadatak gde je visina 5 cm :))), i kao takav ce dosta da se namuce dok ne shvate zasto i kako... (provereno sa ciljnim uzorkom :))) ). Inace neko je na krstarici spominjao poznati metod zvrljanja po lenjiru :), to je mnogo mocna metoda i uz pomoc nje se moze resiti i barem jos trisekcija ugla :))). Naime sve se svodi na sledece: na drvenom lenjiru (pamti li jos takve lenjire), oznacimo dve tacke. e onda se trudimo da svaka od te dve tacke pripada nekoj pravoj a da neka nacrtana tacka pripada pravoj koju "povlaci" lenjir. Ovo je cesto bilo dovoljno da se ljudi zbune oko toga sta znaci konstrusiati lenjirom i sestarom. Ovo gore jeste konstrukcija lenjirom prakticno, ali nije po stogoj formalnoj definiciji :). Da podsetimo sta sve mozemo da radimo u konstrukcijama lenjirom i sestarom: 1. Da lupamo slobodne tacke (znas ono, olovkom lupis po papiru :))) ). 2. Da kroz dve tacke povucemo pravu 3. Da nacrtamo kruznicu tako sto je jedna tacka centar, a druga na kruznici (ostar kraj sestara ... ) 4. Da oznacimo presek dva entiteta (prave i prave, kruznice i ... ) 5. Da na nekom entitetu (prava, kruznica) odredimo tacku koja mu pripada :). Da bi sve ovo bilo potpuno negde imamo dve tacke za koje znamo da je mera njihovog rastojanja 1. Cisto da primetimo ne mozemo lako ni da konstruisemo prav ugao :), zar ne ? Sve u svemu postoji resenje za zadati zadatak, ali sumnjam da ce ga i neko darovito dete iz 6 razreda resiti na onaj nacin :). Zabuna je jer smo svi ocekivali lepo resenje (o Fermaaaaaa gde si sada ti :)) ). Doduse i dato resenje nije bas potpuno cisto, mozda bi moglo do kraja da se uradi samo sa slicnoscu :))). [ 069 @ 01.12.2006. 06:46 ] @
Braker, ne znam kad nije tacno ako je b simetrala a ako b nije simetrala onda nema veze sa zadatkom.
Prema slici to je tacno ali nigde nema simetrale. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|