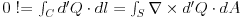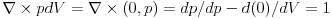[ petarm @ 21.11.2006. 08:17 ] @
| Prvi zakon termodinamike u diferencijalnom obliku d'Q=dU+d'W d'Q,d'W-neegzaktni diferencijali - predstavljaju "male kolicine". dU-egzaktan (neko kaze i totalni) diferencijal Uzmimo primer sirenja gasa pri p=const. d'Q=dU+pdV d'Q=d(U+pV) A H=U+pV je entalpija koja je fja stanja te je dH egzaktan diferencijal. Pa imamo da je d'Q=dH tj. neegzaktan diferencijal je jednak egzaktnom diferencijalu? Kako ovo objasniti? |