Ponudiću dokaz, ali bih molio da se isti podvrgne pomnoj analizi, jer sam pomalo tanak u teoriji grupa.

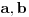
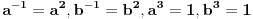
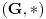
U skupu postoje najmanje dva različita nejedinična i uzajamno neinverzna elementa (jer bi u protivnom imao samo tri elementa). Označimo ih sa . Pošto u grupi devetog reda ciklične podgrupe mogu biti samo trećeg reda, imamo da je . Pretpostavimo da je nekomutativna. Tada na osnovu osobine zatvorenosti zaključujemo da se u nalazi sledećih devet elemenata:



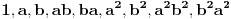
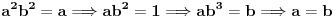
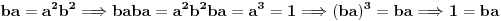
(Napomena: Lako je pokazati da nikoja dva od pobrojanih elemenata ne mogu biti jednaka. Ilustracije radi: , ili , i slično.)

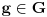
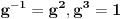
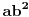
Na osnovu cikličnosti, za svako mora važiti . Na osnovu zatvorenosti, element mora se nalaziti u skupu . Ispitajmo je li to moguće:



















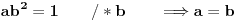
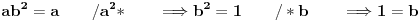
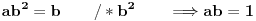
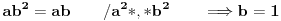
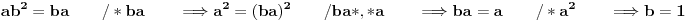
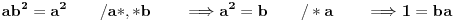
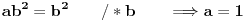
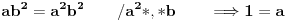
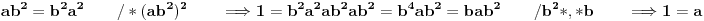
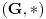
Dakle, osobina zatvorenosti ne može biti zadovoljena, što znači da mora biti komutativna.

_{[Ovu poruku je menjao Farenhajt dana 26.11.2006. u 08:56 GMT+1]}

Mislim da je ovo O.K. Ako pretpostavimo da postoje dva elementa x,y za koje vazi x*y nije isto sto i y*x daljim petljanjem dolazimo do cinjenice da u grupi imamo makar 10 elemenata sto je nemoguce.