Evo ja cu pokusati rijesiti drugi, naravno matematickom indukcijom, a rjesenje prvog proizilazi iz njega, jer je
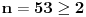
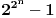
Treba dokazati da je djeljivo sa 15.
1. Provjerimo za prvih nekoliko prirodnih brojeva:
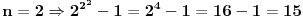
sto je djeljivo sa 15
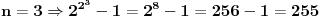
sto je djeljivo sa 15
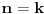
2.Pretpostavimo da je za dati izraz djeljiv sa 15, odnosno
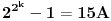
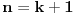
3. Na osnovu pretpostavke dokazemo djeljivost za , odnosno
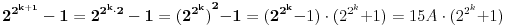
sto je naravno djeljivo sa 15, jer je broj 15 faktor.
Ja se nadam, da sam pomogao, i da nisam negdje pogrijesio.

_{[Ovu poruku je menjao Kolins Balaban dana 27.11.2006. u 13:49 GMT+1]}

Treci zadatak je posledica Ojlerove teoreme koja glasi : Ako su a i b uzajamno prosti brojevi tj. nzd(a,b) = 1,
onda vazi (a^phi(b) - 1) mod b = 0. Ako su a i 11 uzajamno prosti,vazice teorema. phi(b) je Ojlerov broj za broj b.
Potrazi po literaturi dokaz teoreme.Ili na Internetu.

Mladen.

Hvala !!!

Inače, možete li mi preporučiti neku knjigu u kojoj su detaljno obrađeni polinomi.

_{[Ovu poruku je menjao eruanntion dana 27.11.2006. u 01:10 GMT+1]}