Evo opet cu ja pokusati da pomognem.
Usporedni kriterij:
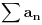
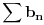
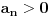
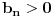
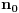
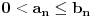
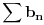
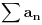
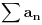
Pretpostavimi da su zadani redovi i , pri cemu je , i neka je od nekog indexa ispunjen uvjet nejednakosti , tada iz konvergencije reda slijedi konvergencija reda , a iz divergencije reda slijedi divergencija reda .

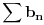
RJESENJE:
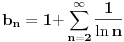
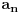
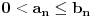
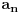
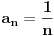
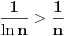
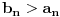
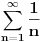
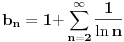
Mi imamo da je npr . Prema datom kriteriju, moramo naci red , za koji je ispunjen uslov , a da pri tome znamo konvergenciju reda, sa kojim poredimo dati red(tj. konvergenciju reda ). Ja cu uzeti npr. da je , jer je sigurno , odnosno , a znamo da red tzv. harmonijski red DIVERGIRA, pa prema tome, i zadati red divergira prema poredbenom kriteriju. Eto, opet se nadam, da sam pomogao, i da nisam pogrijesio. Nekad sam na elt radio redove, ali nisam polozio Analizu I, prebacio sam se na drugi laksi fax.