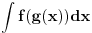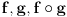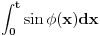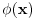[ qzqzqz @ 03.12.2006. 16:13 ] @
|
[ Mlatko @ 03.12.2006. 23:02 ] @
pa.. uglavnom su funkcije pod integralom slozene?! Zato se i koriste raznorazne metode, od supstitucije pa dalje..
Mozda da navedes konkretan primjer iz fizike koji te muci? [ uranium @ 03.12.2006. 23:14 ] @
Pa u opštem slučaju, to je težak problem, jer eto za:
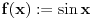 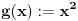 imamo integrabilnost f-ja  , ,  i i 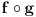 , ali , ali 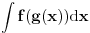 nije elementarna f-ja... nije elementarna f-ja...Postoje razne tehnike izračunavanja integrala, ali mislim da je tebi zapravo potreban sledeći Stav (o smeni promenljive) Neka su  i i  intervali, neka je intervali, neka je 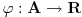 takva da je takva da je 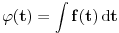 i neka je i neka je 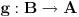 diferencijabilna na diferencijabilna na  . Tada je . Tada je 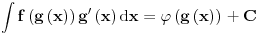 . .Dokaz je pravolinijski, pa prvo probaj sam. Primer: 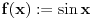 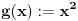 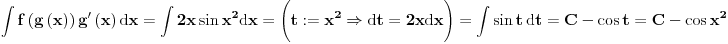 [Ovu poruku je menjao uranium dana 04.12.2006. u 00:28 GMT+1] [ qzqzqz @ 08.12.2006. 15:54 ] @
[ uranium @ 08.12.2006. 19:14 ] @
I ja koliko znam, u opštem slučaju je aproksimacija najbolje što možemo da uradimo...
Eto primera radi, za 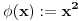 , dobijamo jedan od Frenelovih integrala... , dobijamo jedan od Frenelovih integrala...Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|