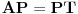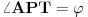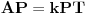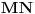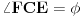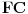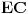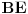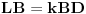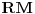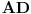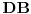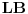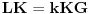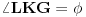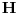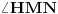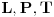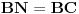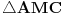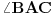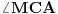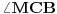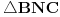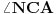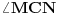|
|
[ badzevic @ 06.12.2006. 06:42 ] @
|
| pozdrav svima
Neka su dati kruznica k, prava p i tacka A van p. Na pravoj p konstruisati tacku P takvu da je |AP|=|PT|, gde je T dodirna tacka kruznice k i tangente na nju povucene iz P.
mozda gresim ali cini mi se kao jako tesko
ima li neko inspiraciju |
[ braker @ 06.12.2006. 10:49 ] @
Izgleda da mogucnost reshavanja zavisi od izbora tachaka A i T,kao i polozhaja prave p,pa povedi rachuna:)
Uglavnom,mislim da je moguce reshiti zadatak na sledeci nachin:
Spojish tachke A i T,nadjesh simetralu duzhi AT,iz te tachke (polovina duzhi AT) normalno na AT povuchesh liniju-mesto preseka sa pravom p daje tachku P.
[ badzevic @ 06.12.2006. 18:54 ] @
nisi pazljivo citao
tacka T nije data
tacka T je jednostavno dodirna tacka kruga i tangente koja se povlaci iz tacke P koju treba konstruisati
dakle treba naci P na zadatoj pravoj p takvu da je odstojanje od dodirne tacke na tangenti jednako odstojanju od zadate tacke A
nisam sposoban ovo da resim
[ badzevic @ 07.12.2006. 00:41 ] @
ah
uz omanje konsultacije pojavilo se elegantno resenje
inverzija u odnosu na krug. preslikamo li tacku A inverzno u odnosu na k dobijamo tacku A'. buduci da inverzija ostavlja invarijantne kruznice koje su normalne na k, takva ce biti kruznica k' koja sadrzi A i A'.
sada se zadatak svodi na konstruisanje k' jer su u njenoj presecnoj tacki sa k poluprecinici od k i k' ortogonalni pa je ta tacka upravo tacka T tj taj polucprecnik od k' je upravo tangenta od k
zato je centar k' upravo trazena tacka P jer je tada |TP|=|PA|
da bismo konstruisali k' potrebna nam je jos jedna tacka, pa posto zelimo da P pripada p, jednostavno cemo A preslikati simetricno u odnosu na p i tako dobiti A''
tako je k' odredjena tackama A, A' i A'', tj P se nalazi u preseku prave p i simetrale duzi A'A''
evo radosti za one koji su se zainteresovali za ovaj zadatak (ukoliko ih ima)
[ Bojan Basic @ 09.12.2006. 16:22 ] @
Evo sličnog zadatka, rešenje prethodnog je stvarno lepo bila bi šteta da se brzo izgubi. :)
Zadatak 2:
Dato je: kružnica  , tačka  , ugao  . Naći tačku  takvu da je 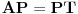 , gde je  dodirna tačka kružnice  i tangente na nju povučene iz  , pri čemu je 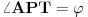 .
Kome je ovo lagano može da proba i malo zakomplikovanu verziju.
Zadatak 3:
Dato je: kružnice  i  , ugao  . Naći tačku  takvu da je 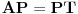 , gde su  i  dodirne tačke kružnica  i  i tangenta na njih povučenih iz  , redom, pri čemu je 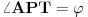 . [ badzevic @ 09.12.2006. 18:07 ] @
evo na brzaka samo da odgovorim na prvi izazov drugi ce sacekati kad budem imao vise vremena
zadrzacemo iste oznake, samo je mala varijacija na temu, isto konstruisemo A' inverzijom na krug, uz tu razliku sto k' sada trazimo pod drugim uslovima
kako je prava AA' tetiva trazene kruznice, periferijski ugao nad njom ce biti jednak polovini centralnog, a centralni je upravo dati fi
stoga provlacimo kroz A proizvoljnu pravu, i na nju iz A' spustamo pravu pod uglom od fi/2, neka je njihov presek neka tacka A''
trazena tacka P je sada centar kruga k' odredjenog tackama A, A' i A''
treci zadatak ce dobiti tretman kasnije u toku veceri
[ badzevic @ 09.12.2006. 18:30 ] @
ne valja bre ovo
fi je ugao nad tetivom AT, ne AA', brljam
sacekajmo veceras
[ badzevic @ 09.12.2006. 18:56 ] @
jel moze ovako
ugao <A'TA je jednak polovini ugla <A'PA, jer su oni centralni i periferijski uglovi hipoteticne kruznice k'
analogno ugao <A'AT je polovina ugla <A'PT
kako je <A'PT + <A'PA = fi, to je <A'TA + <A'AT = fi / 2
pa je ugao <AA'T= pi - fi/2
dakle
inverzijom nalazimo A'
iz A' povlacimo pravu pod uglom pi - fi/2 u odnosu na pravu AA'
tacka T je tada presek ove prave sa kruznicom k
sada je trazena tacka P srediste kruznice k' odredjene tackama A, A' i T
da li sam opet nesto zabrljao?
[ Bojan Basic @ 09.12.2006. 19:26 ] @
Sad je OK (ako nisam i ja nešto prevideo). Ostaje treći zadatak (da napomenem, postoji i četvrti, za kraj  ). [ badzevic @ 10.12.2006. 16:49 ] @
sve mi se nesto cini da resenje zadatka broj 3 (ko li ga je smislio) nije jednoznacno, vec ih avaj ima beskonacno
probacu da poduprem ovo
preslikajmo kruznicu k2 inverzijom u odnosu na k1, dobijamo kruznicu k2'. slika od PA, tangente k2, ce biti neka kruznica, obelezimo je sa Kpa, koja ce dodirivati k2' i prolaziti kroz centar inverzije O.
upravo u ovom trenutku mi se cini da lezi uzrok viseznacnosti resenja, jer izgleda da je izbor takve kruznice proizvoljan, dok god cela lezi unutar k1, a takvih ima i dalje beskonacno mnogo
slika tangente na k1, PT, bice takodje kruznica, obelezicemo je sa Kpt, koja iznutra dodiruje k1 u tacki T i prolazi kroz O, ali takodje se i sece sa Kpa pod uglom fi, jer ako se ne varam kruzna inverzija cuva uglove
konstrukcija dakle tece ovako, nakon sto smo preslikali k2 i uzeli proizvoljno Kpa (ali takvu da je unutar k1), povlacimo na nju tangentu t iz O, i zatim takodje iz O, pravu p pod uglom fi u odnosu na t
prava p je sada tangenta kruznice Kpt u tacki O, kruznice koja treba da dodiruje iznutra k1, pa zato povlacimo normalu na p u O i u njenom preseku sa k1 dobijamo tacku T
centar od Kpt je zato polovina duzi OT
druga presecna tacka tako dobijenih kruznica Kpa i Kpt (pored O koja i ionako ne figurise jer nema konacnu inverznu sliku) bice slika P' trazene tacke P, pa dakle resenje nalazimo inverznim preslikavanjem tacke P' u odnosu na k1
ukoliko ova prica ima smisla, najavljeni zadatak broj 4 bi mogao da glasi ovako:
koju krivu predstavlja geometrijsko mesto svih tacaka P sa trazenim svojstvima?
[ Bojan Basic @ 10.12.2006. 18:15 ] @
Ne valja baš. Nigde se nisi obezbedio da bude 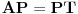 . [ badzevic @ 11.12.2006. 20:30 ] @
mmmm da.. jes tacno
i k2 i k2' sadrze po tacku koja se nalazi na kruznici k' koju jurim da konstruisem, ali nista mi ne garantuje da je jedna od njih slika one druge, a to se mora desiti
znaci radio bih jos na ovome ali moram priznati da u ovom slucaju znatizelja nadjacava strpljenje
stoga ajde, cujmo resenje
fusnota: znaci li ovo da je resenje ipak jednoznacno?
[ Bojan Basic @ 12.12.2006. 11:23 ] @
Nema problema, onda ću odmah dati rešenje četvrtog zadatka, koji je samo uopštenje trećeg pa se ova konstrukcija može primeniti i na njega (a i na drugi, koji je specijalan slučaj trećeg).
Zadatak 4:
Dato je: kružnice  i  , ugao  , realan broj  . Naći tačku  takvu da je 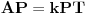 , gde su  i  dodirne tačke kružnica  i  i tangenta na njih povučenih iz  , redom, pri čemu je 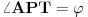 .
Rešenje:
Neka su  i  centri kružnica  i  , redom. Iz proizvoljne tačke  na pravoj 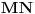 povucimo normalu na tu pravu. Iz proizvoljne tačke  ove normale konstruišimo ugao 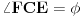 ( dve mogućnosti). Povucimo sada tangentu u tački  , paralelnu sa 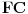 , na kružnicu  ( dve mogućnosti); neka ova tangenta seče 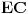 u  . Odaberimo  na pravoj 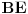 tako da je 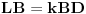 . Nađimo sada  na 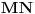 tako da je duž 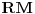 jednaka poluprečniku kružnice  ( dve mogućnosti). Sa centrom u  i poluprečnikom 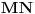 , opišimo kružnicu koja seče 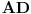 u  ( dve mogućnosti). Kroz  povucimo pravu paralelnu sa 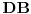 , i neka je njen presek sa 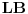 tačka  . Uočimo da je 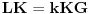 i da je 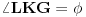 . Iz  povucimo pravu paralelnu sa 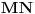 ; s centrom u tački  i poluprečnikom 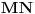 opišimo kružnicu, koja seče ovu pravu u tački 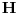 . Pošto je, za odgovarajući izbor tačke 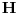 , četvorougao  paralelogram, kružnica koja prolazi kroz  i s centrom u 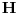 podudarna je s kružnicom  , i nalazi se na istom rastojanju od kružnice  . Dakle, dovoljno je rotirati tačke 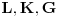 oko tačke  za 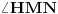 , i dobićemo tačke 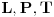 , redom.
Primetimo da ima ukupno šesnaest mogućnosti za ovu konstrukciju. Međutim, posle završne rotacije, neka rešenja će se poklopiti, ostavljajući nam ukupno osam različitih tačaka  , u opštem slučaju. Evo slike jedne od njih.
[att_img]
Brzo smo rešili ove zadatke, nisu ni dospeli na listu nerešenih. :) [ Tijana @ 14.12.2006. 14:29 ] @
Potrebna mi je pomoc oko zadatka za 6. razred za takmicenje.
U pravouglom trouglu ABC na hipotenuzi AB date su tacke M i N tako da je AM=AC i BN=NC. Odrediti ugao MCN.
Svaki savet bi mi znacio.
Hvala
[ Farenhajt @ 14.12.2006. 14:40 ] @
Citat: Tijana: ...tako da je AM=AC i BN=NC.
Koliko vidim, posredi je greška: Treba da bude 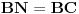 .
Uputstva: Kakav je po vrsti 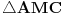 ? Ako 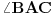 obeležimo sa  , kako će glasiti izraz za 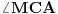 ? A kako će onda glasiti izraz za 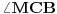 ?
Slično razmatranje primenićemo i na 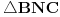 da bismo našli 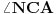 . Kad smo našli ta dva ugla, kako će glasiti izraz za 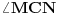 ? Kako taj izraz možemo uprostiti?
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|