Mene u stvari zanima dokaz ove teoreme. P.P. da se u dokazu koristi Gausov zakon.

Da probam za tackasto naelektrisanje.

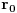
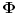
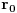
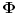
Ako se doticno naelektrisanje nalazi u stabilnoj ravnotezi u tacki , onda mora da se nadje u minimumu elektrostatickog potencijala koji prave druga naelektrisanja. Onda u izesnom ortonormalnom koordinatnom sistemu x-y-z centriranom na mozemo mozemo pisati:

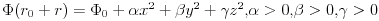
Medjutim, onda

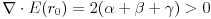
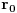
sto se ne slaze (Gausov zakon) sa cinjenicom da se osim naseg probnog naelektrisanja u tacki nemamo druga naelektrisanja.

Ovo sto si dole napisao bi trebalo da predstavlja Gausov zakon u diferencijalnom obliku. Odnosno divE=ro/epsilon nula. Gde je ro prostorna gustina naelektrisanja. Mislim da je ocevidno da sem probnog nael. nemamo drugih nael. u r₀. Mozda si mislio u okolini r₀. Odnosno ako posmatram da u okolini tog nael. nema drugih nael. dobijem iz Gausovog zakona da je fluks nula. A da bi postojala stabilna ravnoteza nuzno je da sve linije sila budu uperene ka probnog naelektrisanju. Pa zato nema stabilne ravnoteze akko nema dejstva spoljasnjih sila. Jesam li u pravu? Voleo bih da malo vise prodiskutujes ovaj svoj dokaz. Unapred hvala

Da bih proucio kretanje probnog naelektrisanja u polju drugih, razmatram samo polje tih drugih naelektrisanja (bez probnog).
Onda zakljucujem da bi probno naelektrisanje bilo u ravnotezi u tacki , polje drugih naelektrisanja (koje se nalaze dalje od ) mora biti takvo da u tacki .

Ali, onda po diferencijalnom obliku Gausovog zakona zakljucujemo da se neko od tih ne-probnih naelektrisanja mora nalaziti u tacki . Kontradikcija.