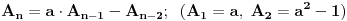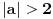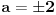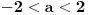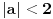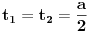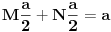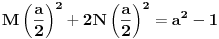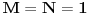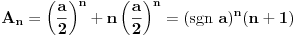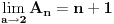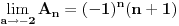Ti si samo postavio rekurentnu formulu. Očekuje se i da je rešiš.






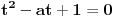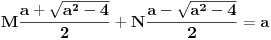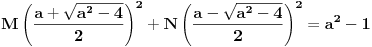Rešavanjem ovog sistema dobijaš: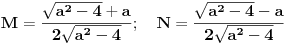



Prema tome, rešenje determinante je: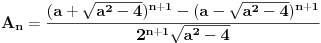



Ako ti je ovo za domaći pa profesor neće da prihvati rešavanje rekurentne jednačine (recimo, ako to još niste učili), ti se „napravi lud“ pa počni od ovog rešenja što sam ti dao i dokaži ga indukcijom.

_{[Ovu poruku je menjao Bojan Basic dana 12.12.2006. u 12:38 GMT+1]}

Bojane, možda ne bi bila zgoreg i mala diskusija o rešivosti? Tvoje rešenje važi samo ako , ali šta se dešava za i za ? (Zadatak ničim ne ograničava domen za .)

Dodatak: Tj. nominalno formula važi i za , ali se može uprostiti.

Stvarno hvala na iscrpnim objašnjenjima. : )
To danas čini nedostatak literature..

Ne znam da li je Bojan prevideo moju prethodnu poruku?

Za nema nikakvih problema. Za ću rešiti sad.







Rešavanjem ovog sistema se dobija (naravno, vodeći računa da je ):



Prema tome, rešenje determinante je:



Međutim, možda nije zgoreg napomenuti da je suvišno čak i ovo izdvajati kao poseban slučaj, jer je lako proveriti da je i .

Stoji ovo poslednje što si rekao, ali je poenta više bila u tehnici rešavanja rekurzivnih jednačina, gde se po pravilu slučaj višestrukih korena zasebno obrađuje

Skoro sam nešto kopao po knjizi The theory of determinants in the historical order of development - Thomas Muir i naišao na jedno uopštenje ovog zadatka:



To uopštenje se pojavilo u radu iz 1878. - Scott R. F., On some symmetrical forms of determinants, Messenger of Math, viii. pp. 131-138., rešenje tog dela je naravno primena identične tehnike koju je već opisao Bojan Basic a u momentu kad se pojavilo nije izazvalo pohvale, jer je rezultat izgleda većim delom već bio poznat.

Takođe, u knjizi A book of mathematical problems - Wolstenholme J. iz 1867. kao jedan od zadataka pojavljuje se izračunavanje determinante: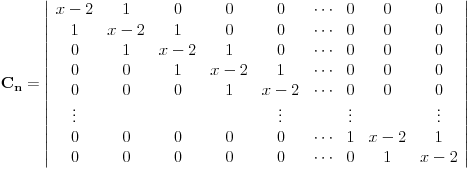



Na kraju, da pomenem da postoji direktna veza između polazne determinante 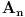i Čebiševljevih polinoma druge vrste a to nam daje još nekoliko formula za izračunavanje 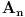- za detalje pogledati Chebyshev Polynomial of the Second Kind

_{[Ovu poruku je menjao uranium dana 14.12.2006. u 07:14 GMT+1]}