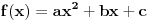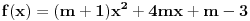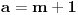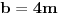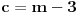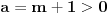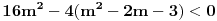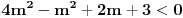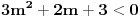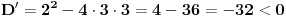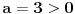[ dalmasica @ 15.12.2006. 16:06 ] @
| Za koje realne vrijednosti od m polinom f(x)=(m+1)x^2+4mx+m-3 prima pozitivne vrijednosti za svaki m Є R? rješenje: Da bi polinom primao pozitivne vrijednosti treba biti: D<0 m+1>0 nakon računanja diskriminante dobivamo D = 4(3m^2+2m+3) sada provjeravamo kakve vrijednosti prima funkcija 3m^2+2m+3 D2 = 4-4*3*3 = -32 3>0 odvade slijedi da je 3m^2+2m+3 > 0, dakle D>0, pošto je uvjet da je D<0 to jr rješenja prazan skup!? U testu mi je stavio polovično rješenje, gdje sam pogriješila, ako ko zna recite mi ili možda drugi način rješavanja, plllliiiiiiiiizzzzzzzzzzz? Unaprijed hvala!!!! |