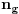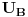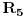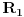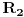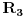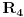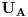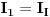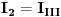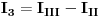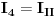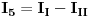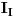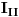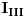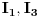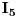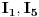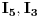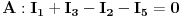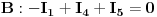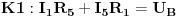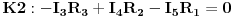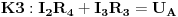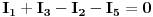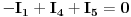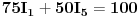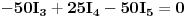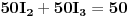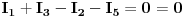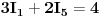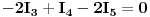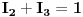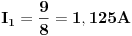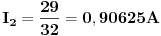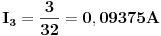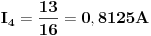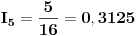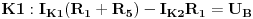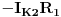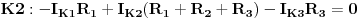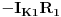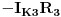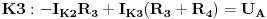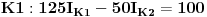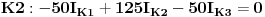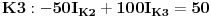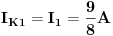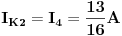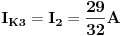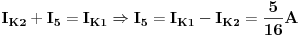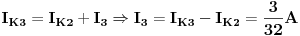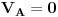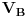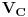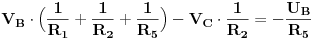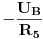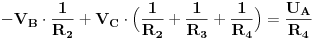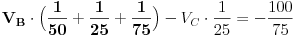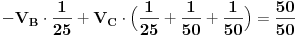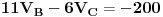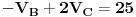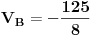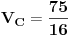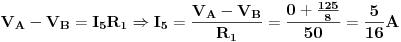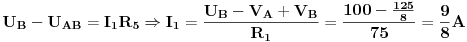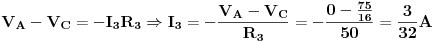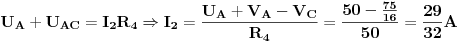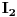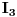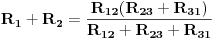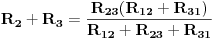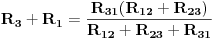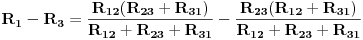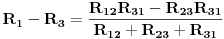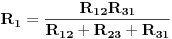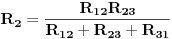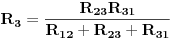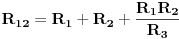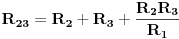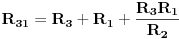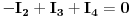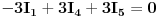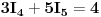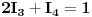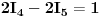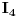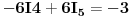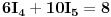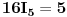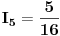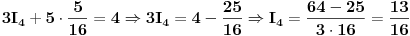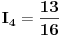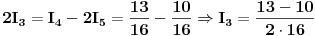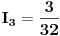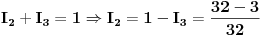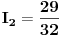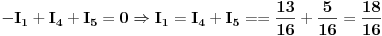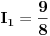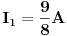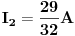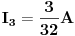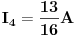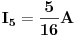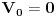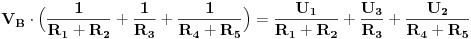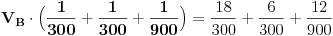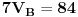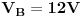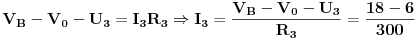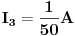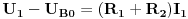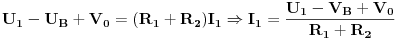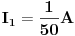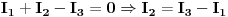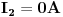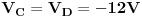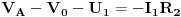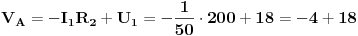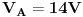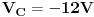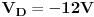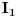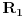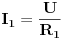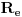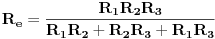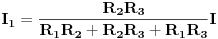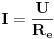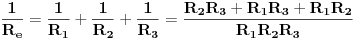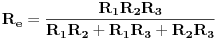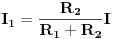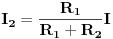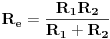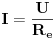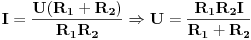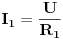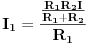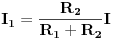|
|
[ dines7 @ 17.12.2006. 17:40 ] @
|
| Pozdrav!
Uz dugo googlanje i pretrazivanje ove stranice dodjem na ideju da se obratim forumskoj zajednici za pomoc u rijesavanju sljedeceg zadatka.Za mnoge ovo ne predstavlja ni "p" od problema ali ja ,na zalost ,jos ne vladam principima rijesavnja ovakvih strujnih kola te stoga molim sve one koji su u mogucnosti(vrijeme i volja) da mi pomognu, ako je ikako moguce "step-by-step" metodom.
Radi se o ovom kolu:

Traze se pojedinacne struje u granama. |
[ darkon @ 18.12.2006. 14:14 ] @
Postoji nekoliko metoda rešavanja električnih kola. Tu su metoda direktnom primenom Kirhofovih zakona, metoda konturnih struja i metoda potencijala čvorova. Referentna literatura iz te oblasti je npr. Branko Popović, Osnovi elektrotehnike I.
Prema metodi konturnih struja, nacrta se graf električnog kola i odredi se broj grana i broj čvorova. Od 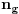 jačina struja u 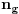 grana grafa, nezavisno je samo:
 ,
gde je 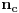 broj čvorova grafa električnog kola.
Prema tome, ovo je broj nezavisnih kontura koje se mogu izabrati u grafu, tj. broj konturnih struja.
U grafu ekvivalentnom ovom električnom kolu imamo pet grana i tri čvora, pa prema gornjoj jednačini imamo tri konture.
Njih biramo tako da je prva kontura ona koju određuju grana sa izvorom 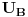 i otpornikom 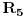 i grana u kojoj je otpornik 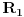 ; druga konrura je ona koju određuju grane sa otpornicima 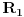 , 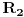 i 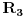 ; treću konturu određuju grane sa 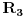 , 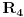 i 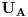 (smer kontura je određen smerom obrtanja desnog zavrtnja).
Postavi se sistem tri jednačine sa tri nepoznate (jačine konturnih struja). Kada se odrede konturne struje, određuju se struje grana na sledeći način:
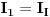 ,
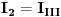 ,
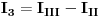 ,
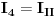 ,
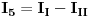 ,
gde su:
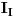 , 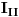 i 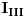 struje kontura 1, 2 i 3, respektivno. [ Kolins Balaban @ 20.12.2006. 21:09 ] @
Evo pokusat cu ja rijesiti ovo kolo. Slika na kojoj su oznacene konture je prikazena uz poruku.
Prema prvom KZ za dato kolo postavljas  jednačine. Mozes uzeti bilo koja dva čvora (ja sam uzeo čvorove A i B). Ako struja ulazi u čvor, stavljas joj predznak + (npr. u čvor A ulaze struje 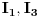 pa imaju predznak +, a struja 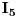 izlazi, pa ima predznak -) Prema drugom KZ postavljas onoliko jednačina, koliko imaš kontura, odnosno tri jednačine za konture K1, K2 i K3. Smjerove obilaženja kontura određujes proizvoljno, a ja sam uzeo da su sve u smjeru kazaljke na satu. Ako se smjer oblilaženja konture i smjer struje u grani podudaraju, uzimas predznak + (npr. za smjer konture K1 i smjerove struja 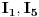 ), a ako se mimoilaze, onda uzimas predznak - (npr. za smjer konture K2 i smjerove struja 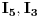 ).
[att_img]
Jednačine po prvom KZ-u (za čvorove A i B) su:
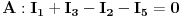
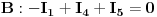
Jednačine po drugom KZ-u (za konture K1, K2 i K3) su:
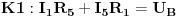
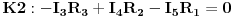
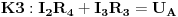
Uvrštavanjem brojčanih vrijednosti, u dobijene jednačine, dobit ćemo sljedeći sistem jednačina:
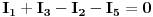
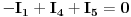
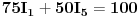
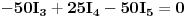
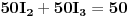
Dijeljenjem treće i četvrte jednačine sa 25, a pete sa 50, imamo sljedeći sistem jednačina:
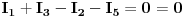
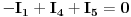
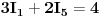
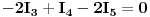
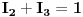
Rješavanjem ovog sistema, dobijamo struje:
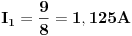
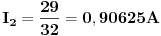
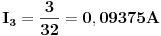
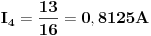
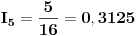
PS: Bio sam napravio jednu greskicu, ali sam je naknadno uocio i popravio.
[Ovu poruku je menjao Kolins Balaban dana 23.12.2006. u 02:07 GMT+1][ cicika @ 21.12.2006. 12:45 ] @
Citat: Predznak - kod struje govori da je smjer te struje u kolu pogrešno predpostavljen, i da ga treba promjeniti.
Ne treba ga menjati, samo treba imati u vidu da je ta struja suprotnog smera. [ Kolins Balaban @ 21.12.2006. 14:48 ] @
da, pogresno sam se izrazio, mislio sam reci da u šemi treba promjeniti smjer struje, ili u rješenju samo dopisati, da je on pogrešno pretpostavljen.Hvala na ispravci ;)
[ Kolins Balaban @ 23.12.2006. 01:48 ] @
Evo, rijesit ću dato kolo i metodom konturnih struja. To je u stvari redokovani metod Kirhofovih zakona, koji smanjuje broj jednacina, na onoliko, koliko imamo kontura. U nasem slučaju će to biti tri jednačine. Prema tome, trebamo naći tri struje, za svako konturu po jednu. Te struje ću označiti sa 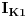 (za prvu konturu), 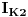 (za drugu konturu) i 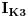 (za treću konturu). Konturna struja 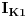 predstavlja struju kroz nezavisnu granu (to je ona grana struje koja pripada SAMO toj konturi, znači ni jednoj drugoj) prve konture, struja 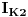 predstavlja struju kroz nezavisnu granu druge konture itd. Te struje sam naznacio na slici. Smjer konturne struje u nezavisnoj grani kao i smjer obilazenja konture, mozemo uzeti proizvoljno, ali je lakše ako se uzmu isti smjerovi.
[att_img]
Jednačine konturnih struja su sljedeće:
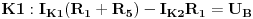 znači, struju u prvoj konturi smo pomnožili sa sumom SVIH otpora u toj konturi, a zatim tom naponu dodali drugu konturnu struju pomnoženu sa otporom u ZAJEDNIČKOJ grani za prvu i drugu konturu, pazeći na smjer obilaženja kontura (vidimo da se smjer prve konture i smjer druge konture mimoilaze u zajedničkoj grani - grani sa otpornikom 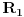 , pa je zato 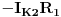 ). Naravno, sa desne strane jednačine nam se nalaze sve elektromotorne sile u toj konturi, a njihov predznak određuje smjer obliaženja konture, kao i kod IIKZ. Na isti način dobijemo i ostale dvije jednačine:
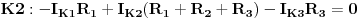 (prva i druga kontura se mimoilaze u zajedničkoj grani sa otpornikom 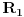 , pa je zato 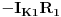 , a druga i treća kontura se mimoilaze u zajedničkoj grani sa otporikom 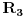 , pa je zato 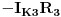 )
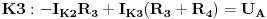
Uvrštavanjem brojčanih vrijednosti dobijemo sljedeći sistem jednačina
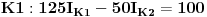
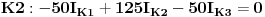
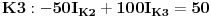
Rješavanjem ovog sistema dobijemo da je:
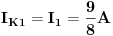
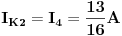
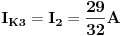
Sada za čvor B prema I Kirhofovom zakonu imamo da je:
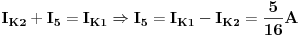
Za čvor C je
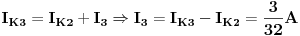
Sljedeći puta ću riješiti isto kolo i metodom potencijala (napona) čvorova. [ Kolins Balaban @ 23.12.2006. 15:09 ] @
Evo i metode potencijala čvorova. Poenta ove metode je da se jedan od čvorova proglasi referentim (uzemljimo ga, odnosno stavimo da potencijal tog čvora iznosi 0), i u odnosu na taj referentni čvor odredimo potencijale ostalih čvorova. Koristit ću istu sliku, kao u prethodnom postu. Obično uzemljujemo onaj čvor, u koji se stiče najvise grana. U ovom kolu je to čvor A, pa ću staviti da je 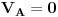 . Prema tome, treba odrediti potencijale 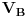 i 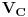 , tj. postaviti dvije jednačine.
Jednačine se postavljaju na sljedeči način: SA LIJEVE STRANE JEDNAČINE: potencijal čvora A puta suma provodnosti SVIH grana koje se stiču u taj čvor MINUS (znači uvijek minus) potencijali ostalih čvorova pomnoženi sa onom provodnisti koja veže taj čvor sa čvorom A.SA DESNE STRANE JEDNAČINE: Suma svih struja koje se stiču ili otiču iz tog čvora. Evo kako izgleda ta jednačina za čvor B
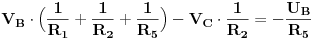
Znači, potencijal čvora B smo pomožili sa sumom provodnosti svih grana vezane za taj čvor i od toga ODUZELI potencijal čvora C pomožen sa provodnošću grane koja veže čvor B i čvor C. Vidmo da je izvor 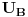 vezan - polom na čvor B, odnosno odvodi struju iz tog čvora, naravno kroz otpornik 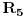 , pa je zato 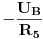 . Jednačina za čvor C ima sljedeći oblik:
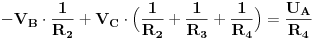
PREDZNAK + SVAVLJAMO SAMO UZ ONAJ POTENCIJAL CVORA, ZA KOJI PIŠEMO JEDNAČINU!!
Uvrštavanjem brojčanih vrijednosti u prethodne dvije jednačine, dobijemo:
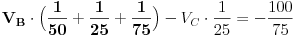
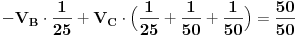
Množenjem prve jednačine sa 150, a druge sa 25, dobijemo:
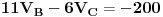
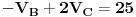
Rješenje ovog sistema je:
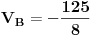
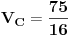
Sa slike se vidi da je
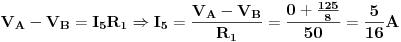
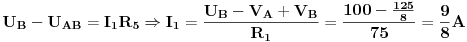
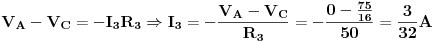
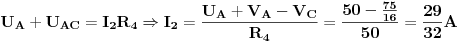

Bilo bi super, kad bi neko nasao vremena, da u ovoj temi za dato kolo odredi jednu ili dvije struje Tevenenovom teoremom, Nortonovom teoremom (jer se ovih 5 metoda najviše koriste), a može i Milmanovom teoremom, metodom superpozicije itd., pa da se na jednom mjestu nađu lijepo objašnjene sve metode rješavanja električnih kola na ovom primjeru. Siguran sam, da će mnogima dobro poslužiti, i da će biti mnogo manje novih postova sa ovom problematikom.
Pozz!
[Ovu poruku je menjao Kolins Balaban dana 24.12.2006. u 12:09 GMT+1][ Black3maj @ 02.01.2007. 20:37 ] @
Kada smo kod stalnih struja,moze li neko da mi objasni transfiguracije otpornickih mreza........
[ Kolins Balaban @ 03.01.2007. 14:35 ] @
Opet ja. Pokušati ću odgovoriti na tvoje pitanje.
[att_img]
Kontura koja se sastoji od tri otpora 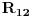 , 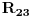 i 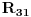 i koja posjeduje tri čvora 1, 2. i 3, obrazuje spoj otpornika u trougao koji je prikazan na slici. Spoj otpora u zvijezdu, također prikazan na slici, obrazuje tri otpora 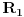 , 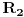 i 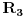 čiji je jedan kraj povezan u zajednički čvor 0, a drugi u pretpostavljenim čvorovima spoja trougla 1, 2. i 3 respektivno. Transfirugacija između ova dva spoja moguća je samo pod uslovom da se u čvorovima 1, 2. i 3. održe iste vrijednosti potencijala 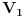 , 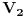 i 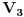 , da se održe iste vrijednosti struja 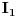 , 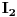 i 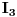 koje se u njima stiču, i da se održe jednake vrijednosti ulaznog otpora između čvorova 1. i 2 zatim 2. i 3. i na kraju 3. i 1.
Kod spoja u zvijezdu, ako se izvor priključi između čvornih tačaka 1. i 2, otpori 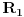 i 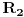 su vezani su srijski i kroz njih protiče ista struja, dok u otporu 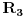 neće biti struje. Ako se isti izvor priključi na spoj u trougao, između istih čvornih tačaka 1. i 2, u tom slučaju, u odnosu na izvor, otpor 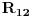 paraleleno je povezan sa rednim spojem otpora 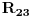 i 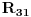 .
Spoj zvijezda i spoj trougao biće ekvivalentni ako su im ulazni otpori između čvornih tačaka međusobno jednaki. Za prethodno opisani slučaj, ako je otpor između tačaka 1. i 2. u spoju zvijezda, jednak otporu između čvornih tačaka 1. i 2. spoja trougao, važi:
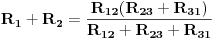
Primjenijući isti postupak za parove čvorova 2 i 3, zatim za 3 i 1, dobijemo sljedeće dvije jednačine:
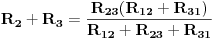
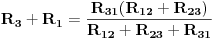
Prema tome dobili smo sistem od tri jednačine, koje u postupku transfiguracije uspostavljaju odnos spoja otpora u trougao u spoj otpora u zvijezdu, i obrnuto. Za poznate iznose opora u jednom spoju mogu se, rješavanjem sistema jednačina, odrediti otpori u drugom spoju.
Ako od prve jednačine oduzmemo drugu, dobit ćemo:
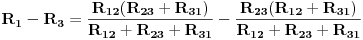
odnosno
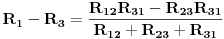
Ako tu jednačinu saberemo sa jednačinom
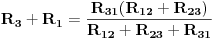
dobit ćemo da je
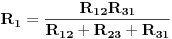
Iz dobijenog sistema, sličnim postupkom, možemo dobiti i ostale vrijednosti otpora:
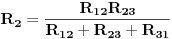
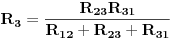
Ako je u pitanju transfiguracija spoja otpora u zvijezdu u ekvivalentni spoj otpora u trogao, rješavanjem dobijenog sistema jadnačina dobija se:
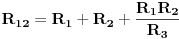
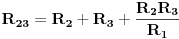
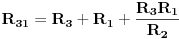 [ dines7 @ 03.01.2007. 21:00 ] @
Odlicni prilozi Kolins! ;)
Sve je potpuno jasno,jedino zahvaljujuci svojoj losoj matematickoj podlozi nisam u stanju da rijesavam sisteme jednacina sa vise nepoznatih,poput ove koju si naveo u prvom primjeru:

Kako se dolazi do rjesenja?
Matrice,Gaus,zamjene...??? [ Black3maj @ 03.01.2007. 21:10 ] @
Kolinse hvala puno....
Sisteme ja resavam putem gausa,u pocetku malo smara al resi par zadataka dok neuhvatis caku,gledaj da prvo eliminises I2,pa I4.......
[ Kolins Balaban @ 03.01.2007. 23:04 ] @
Eh ovako. Riješit ću i taj sistem jednačina jer je sastavni dio zadatka, ali nije na pravom mjestu, pa se nadam da moderator neće obirsati moj post.
Sistem od 5 jednačina, sa 5 nepoznatih je skoro nemoguće riješiti metodom determinanti, jer moraš izračunati 6 determinanti 5-tog reda, i SIGURNO ČEŠ POGRIJEŠITI. Najlakše je kombinovati metodu suprotnih koeficijenata (gausovu metodu) i metodu supstitucije.
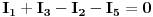
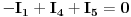
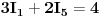
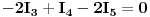
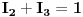
Znači, iz sistema prvo eliminišemo struju 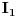 na sljedeći način
1. Saberemo prve dvije jednačine, jer će nam se pokratiti 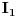 (a vidi sreće i 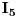 ) pa dobijemo:
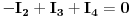 (gledaj da promjenive stavljaš po redu, od manjeg indexa, ka većem)
2. Drugu jednačinu pomnožimo sa 3, i saberemo sa trećom:
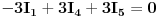
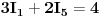
-------------------------+
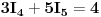
Ostale jednačine u kojima nema 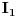 ne diramo, pa imamo sljedeći sistem jednačina:
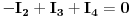
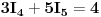
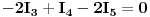
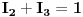
Sada treba eliminirati nepoznatu 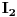 , a to ćemo uraditi tako što saberemo prvu i četvrtu jednačinu, pa dobijemo
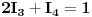
Ostale jednačine u kojima nema 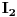 prepišemo, pa dobijemo sljedeći sistem:
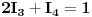
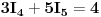
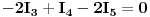
Sada treba eliminirati nepoznatu 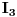 , a to ćemo uraditi tako što saberemo prvu i treću jednačinu, pa dobijemo
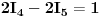
Drugu jednačinu ne diramo, jer u njoj nema 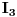 , pa imamo sljedeći sistem
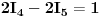
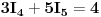
Sada eliminiramo 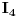 , a to možemo uraditi množeći prvu jednačinu sa -3, a drugu sa 2 (da dobijemo u prvoj -6, a u drugoj 6, uz 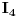 ), ili obrnuto, prvu sa 3, a drugu sa -2. ja ću odabrati prvu varijantu, pa ću dobiti:
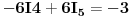
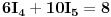
-------------- +
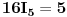
Odakle je
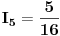
Ako vratimo 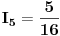 u neku od jednačina sistema
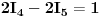
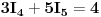
npr. drugu, dobijemo:
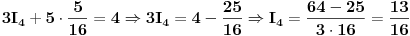
Prema tome dobili smo da je
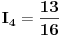
Ako sada 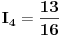 i 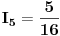 vratimo u jednačinu
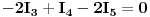
dobit ćemo
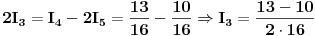
odnosno
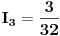
Struju 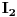 ćemo najlakše dobiti iz jednačine
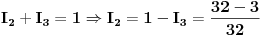
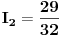
I najzad, struju 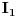 možemo dobiti iz bilo koje prethodne jednačine (jer je svaki sistem dobijen naknadno, ekvivalentan početnom sistemu), a ja ću uzeti jednačinu
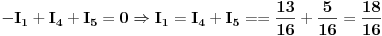
i najzad
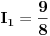
JOŠ DA NAPIŠEM KONAČNA RJEŠENJA, i odoh spavati :D :)
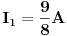
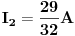
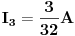
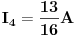
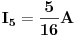 [Ovu poruku je menjao Kolins Balaban dana 04.01.2007. u 00:18 GMT+1]
[Ovu poruku je menjao Kolins Balaban dana 04.01.2007. u 00:18 GMT+1][ dines7 @ 04.01.2007. 09:42 ] @
Kolins,veliko hvala! :o)
[ dines7 @ 05.01.2007. 18:21 ] @
Kako doci do potencijala pojedinih tacki, u ovom slucaju sa A,B,C i D oznacenim , u odnosu na 0-tu tacku?
 [ Kolins Balaban @ 07.01.2007. 10:31 ] @
Pokusat cu ti pomoci jos sada, ali necu vise dok ne vidim gdje si TACNO zapeo, i dokle si ti SAM dosao sa rjesavanjem zadatka. Pri rjesavanju zadatka, koristit cu tvoju sliku, a do nekih cvorova cu doci METODOM POTENCIJALA CVOROVA. Trebas znati, da se u tom kolu nalaze samo DVA cvora, i to cvorovi (cvor je mjesto u elektricnom kolu, gdje se spajaju TRI ili VISE GRANA) B i 0, dok su A, C i D samo TACKE, a ne cvorovi, ali je moguce naci potencijal svake tacke u kolu. Potencijal cvora B cu naci mateodom potencijala cvorova, a za potencijale tacaka A, C i D potrebno je naci struje u kolu. Posto je u zadatku dato da je 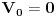 , potrebno je jos naci 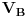 , odnosno napisati jednu jednacinu. Ta jednacina ima oblik:
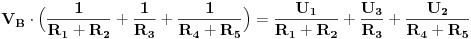
Uvrstavanjem brojcanih vrijednosti, dobijemo sljedecu jednacinu:
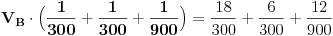
Mnozenjem jednacine sa 900, dobijemo:
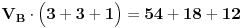
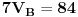
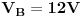
Gledajuci sliku, mozemo sada dobiti struje u kolu:
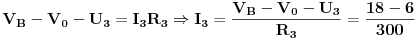
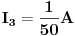
Dalje sa slike imamo da je
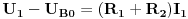
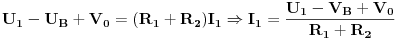
UVrstavanjem konkretnih vrijednosti, dobijemo da je:
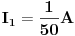
Primjenjujuci prvi KZ na cvor B, mozemo napisati sljedecu jednacinu:
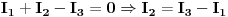
odnosno
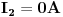
Sada, kad smo nasli sve struje u kolu, mozemo preci na odredivanje potencijala cvorova i tacaka u kolu.
Vec znamo da je
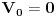
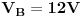
posto je 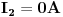 , to je
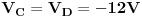 , jer se nalazi direktno na - polu izvora, a nema struje u toj grani da pravi neki pad napona.
Dalje sa slike vidimo da je:
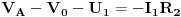
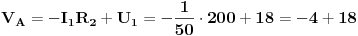
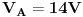
I na kraju da ispisemo sve trazene potencijale:
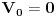
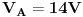
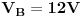
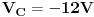
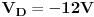
Ja mislim da je to TO. Naravno, nije nuzno da kolo rjesavas metodom potencijala cvorova, mozes koristiti bilo koji nacin opisan u prethodnim postovima. Valjda nisam negdje pogrijesio :( pozz!
[Ovu poruku je menjao Kolins Balaban dana 07.01.2007. u 19:33 GMT+1][ Black3maj @ 06.02.2007. 18:38 ] @
Moze li neko da mi objasni strujni i naponski razdelnik......Hvala
[ R A V E N @ 10.03.2007. 14:32 ] @
Kollins,svaka pohvala za objašnjenja!Izvrsna tema!
[Ovu poruku je menjao R A V E N dana 10.03.2007. u 15:47 GMT+1]
[ R A V E N @ 10.03.2007. 15:54 ] @
Citat: Black3maj: Moze li neko da mi objasni strujni i naponski razdelnik......Hvala
Ovo prvo vjerovatno je Pravilo Raspodjele Struja( Current Divider Rule - CDR).Primjenjuje se u kolima sa paralelnim otpornicima i njegova svrha je da se izračuna jačina struje kroz svaki od tih otpornika ponaosob.Ako imamo slijedeće kolo:

i recimo da moramo pronaći struju 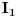 kroz otpornik 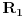 ,tada vrijedi 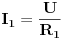 ali vrijedi i  ,gdje je 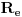 ,naravno,ekvivalentna otpornost gornje veze otpornika 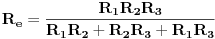 .Sada izraz za 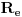 uvrstimo u  pa taj izraz uvrstimo u 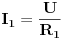 ,izvršimo skraćivanje 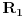 i za struju 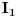 imamo
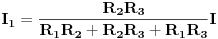
 naravno,nezavisno izračunamo iz 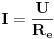 .
Ovo možeš primjeniti za bilo koji broj paralelno vezanih otpornika.
[Ovu poruku je menjao R A V E N dana 18.03.2007. u 18:10 GMT+1][ Kolins Balaban @ 11.03.2007. 23:40 ] @
Mala ispravka kod paralelne veze tri otpornika:
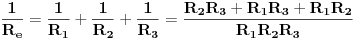
Odakle se dobije da je
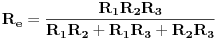
Koliko mogu primjetiti, ti si se zavrtio u krug sa tim formulama, al OK. bitno je samo reci, da strujni djelioc dobijamo paralelnom vezom otpornika, kao na slici u prethodnom postu, jer se tu struja dijeli, prema I KZ, a napon je konstantan na svim otpornicima. Naponski djelioc predstavlja serijska veza otpornika, jer napon na svakom otporniku direktno zavisi od njegovog otpora, dok je struja konstantna kroz sve otpornike. [ R A V E N @ 13.03.2007. 12:22 ] @
U krug? 
Ja sam samo naveo način kako i šta iz čega slijedi,nešto što se izostavi na uobičajenoj nastavi elektrotehnike.Ja barem nisam primjetio da je ikada ovo pravilo specijalno izvođeno a još manje imenovano kao takvo.U knjigama i zbirkama je dat uobičajeni primjer sa dva otpornika:
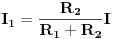
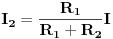
i prosječnim studentima isprva nije jasno na osnovu čega ove dvije formule.
[Ovu poruku je menjao R A V E N dana 13.03.2007. u 13:38 GMT+1][ Kolins Balaban @ 13.03.2007. 14:15 ] @
pa za dva otpornika jeste tako ;)
ekvivalentna otpornost paralelno vezana DVA otpornika je
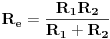 da ne izvodim, to je krajnja formula (samo za paralelnu vezu DVA otpornika u formuli za ekvivalentnu vezu se nalazi ZBIR tih otpornika, dok za TRI I VISE nije tako, a to sam i pokazao u prethodnom postu)
posto je 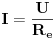 to je
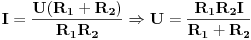 **
struja kroz npr. otpornik 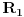 je
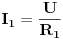
pa kad tu iskoristimo formulu ** dobijemo da je
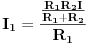 ***
i na kraju se dobije formula koju si i ti napisao
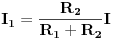
a sad da ti pokazem kako si se zavrtio u krug. ti kazes, da da sad I izracunamo iz formule 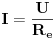 , ako si tu mislio da I uvrstimo u prethodnu formulu (***), onda nisi uradio nista. Sve zavisi sta ti je dato u zadatku ;) i od toga i zavisi put kojim ces krenuti da rjesavas zadatak. (ako ti nije dato U, ili jedan od otpornika, neces moci ni izracunati I). Valjda se sad razumijemo :).
Mislim da ovo nije OK za TRI I VISE OTPORNIKA "- u imeniocu je zbir svih proizvoda "svakog otpornika sa svakim"". Ako imas n otpornika, onda bi se moglo reci da se u nazivniku nalazi suma svih kombinacija n-1-vog razreda od n elemenata. Npr. Ako imas 5 otpornika, onda je to 4. razred od 5 elemenata, imat ces u nazivniku 5 elemenata (racunas ih po formuli 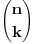 ) gdje je k razred, a n broj elemenata). Naravno, samo izracunas kombinacije indexa, i onda je lako to poredati.
[Ovu poruku je menjao Kolins Balaban dana 13.03.2007. u 15:33 GMT+1][ R A V E N @ 18.03.2007. 16:37 ] @
Jajix!,al` zabrljah:-D...no dobro.
Kolins(usput jednom je bio i nikada više slavni Collins System,hehehe...),ne moraš tako ići u detalje.Bez obzira na previd koji sam napravio,ja sasvim dobro pojmim paralelnu vezu otpornika,Kirhofove zakone,Omov zakon i specijalan slučaj ekvivalentne otpornosti paralelno vezana dva otpornika.
Vrćenja u krug nije bilo jer se 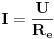 može izračunati nezavisno od onoga što sam prije toga naveo.
[Ovu poruku je menjao R A V E N dana 18.03.2007. u 19:12 GMT+1][ Kolins Balaban @ 19.03.2007. 18:06 ] @
Niko nije ni rekao da ti to ne znas, ali ovo sto si ovdje napisao to nije bilo ok i ispravio sam te. mislim da nije ok, sto se na neki nacin ljutis, sto sam te ispravio. koliko sam to uradio radi tebe, toliko sam to uradio i radi drugih koji NE ZNAJU ono sto si naveo da dobro pojmis ;) meni je ovdje prvenstveno cilj da pomognem onome kome je pomoc potrebna, ako vec mogu pomoci, a nije mi cilj da nekoga ismijavam (cini mi se da si ti to tako shvatio). Pozz
[ R A V E N @ 25.03.2007. 21:22 ] @
Citat: R A V E N: Jajix!,al` zabrljah:-D...no dobro.
Kolins(usput jednom je bio i nikada više slavni Collins System,hehehe...),ne moraš tako ići u detalje.Bez obzira na previd koji sam napravio,ja sasvim dobro pojmim paralelnu vezu otpornika,Kirhofove zakone,Omov zakon i specijalan slučaj ekvivalentne otpornosti paralelno vezana dva otpornika.
Vrćenja u krug nije bilo jer se 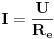 može izračunati nezavisno od onoga što sam prije toga naveo.
[Ovu poruku je menjao R A V E N dana 18.03.2007. u 19:12 GMT+1] [ Igor100 @ 16.12.2009. 20:29 ] @
Molim vas,pomozite mi.Sutra imam kontrolni iz fizike.Treba da mi resite jedan zadatak.
Treba da upotrebljavate Kirhofova pravila:
Otpornici su vezani u trougao.Na svakoj strani se nalazi otpornik od 36 Oma.Treba da se izracuna ekvivalentni otpor.
Koristite gradivo fizike osnovne skole.
Unapred zahvalan.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|