[ Xarios @ 03.01.2007. 16:20 ] @
|
| Pozdrav,
Ako moze pomoc u s vezi sljedeceg zadatka >>
Napomena:
racunao sam ovaj zadatak preko sarusovog pravila (mozda i nije najbolja ideja) ali nece da mi ispadne rezultat nula (0)
zadatak se nalazi u zbirci M.P.Uscumlic (zadatak broj: 888)
>>Izracunati determinantu:

Unaprijed Hvala. |
[ Farenhajt @ 03.01.2007. 16:33 ] @
Opiši svoj postupak - možda si negde napravio računsku grešku, pošto se Sarusovim pravilom takođe lako dobija rezultat 0.
[ bobanex @ 03.01.2007. 16:38 ] @
ukratko:
treba da dobijes z^6 - 2z^3 + 1 sto jeste jednako nuli
[ Xarios @ 03.01.2007. 16:46 ] @
Upravo sam to dobio.
Ali kako da to (z^6 - 2z^3 + 1) bude jednako nuli? to me interesira.
Jel sada uvrstim -1/2 +i ... umjesto Z i racunam.
Ako je tako, ja sam racunao ali ne dobijem nulu.
Ako moze, nekoliko prvih uputa pri daljem racunjanju pa cu ja nastaviti.
[ bobanex @ 03.01.2007. 16:51 ] @
pa tako reci :)
z^6 - 2z^3 + 1 = (z^3 - 1)^2
a z^3 = 1
[ Xarios @ 03.01.2007. 17:15 ] @
Mozda izgledam malo cudno, ali kako dobijes z^3 =1 ?
Jel uvrstavanjem (probao sam nece da ispane 1)?
[ Farenhajt @ 03.01.2007. 17:29 ] @
Mora ispasti 1, nisi dobro računao. Prikaži računicu pa da vidimo gde si pogrešio.
[ bobanex @ 03.01.2007. 17:36 ] @
a bas sam se ponadao da ces nesto i sam da uradis :)
inace z = e^(i*2pi/3)
ajd sad
[ Kolins Balaban @ 03.01.2007. 17:47 ] @
Evo kako se dobije 1.
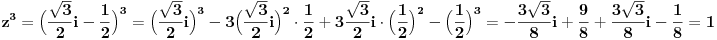
pa je odatle
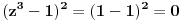
[ Xarios @ 03.01.2007. 17:54 ] @
Sramota, bio sam pogrijesio na sljedecem:
i^3=i^2*i=-1*i=i
umjesto
i^3=i^2*i=-1*i=-i
Hvala velika, kolege!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.