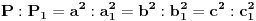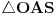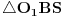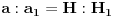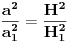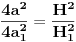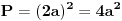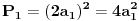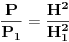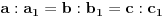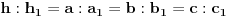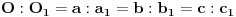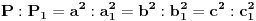Evo ja cu pokusati da odgovorim na tvoje pitanje.
Nisam bas vjest u crtanju, pa se nadam da ce skontati sliku:
[att_img]
S - vrh piramide
a1 - polovina strane manje baze
a - polovina strane vece baze
O - srediste vece baze (presjek dijagonala)
O1 - srediste manje baze (presjek dijagonala)
Iz sličnosti pravouglih trouglova i , slijedi da je

kvadriranjem te jednakosti imamo da je

ako sa lijeve strane i brojnik i nazivnik pomnozimo sa 4, dobijemo

posto je


to je

ono je super!hvala!
cak i ja,koji sa matematikom nisma bas u najboljim odnosima,sam skont'o!
ali ako prof. od mene zatrazi da mu dokazem slicnost pravouglih trouglova,tu postaje gusto.ako mozes,pojasni mi malo to...

Dokazati da su ta dva trougla slicna, je trivijalno. Znam da si slicnost i homotetija rade s pocetka II razreda srednje skole, bar sam ja tad radio. Dovoljno je samo znati sljedece: Dva trougla su slicna ako su im dva ugla jednaka (automatski je jednak i treci). Sada samo primjenis tvrdnju pod a).
Kao sto se moze vidjeti, kod datih trouglova jedan ugao je zajednicki (ugao u vrhu S), i imaju po jedan prav ugao (uglovi u vrhovima O i O1), pa prema tome slijedi da su im jednaki i uglovi u vrhovima A i B.
Ako su dva trougla slicna, tada su:
a) Odgovarajuce stranice su proporcionalne

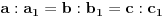
b) njihove odgovarajuce visine proporcionalne sa odgovarajucim stranicama

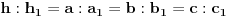
c) njihovi obimi proporcionalni su odgovarajucim stranicama

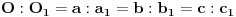
d) njihove povrsine proporcionalne su kvadratima odgovarajucih stranica

Kolins Balaban,
hvala ti mnogo,gde cuo i ne cuo :D