Tvrđenje je posledica sledeće teoreme.

Teorema:

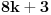
Svaki prirodan broj oblika jednak je zbiru kvadrata triju neparnih prirodnih brojeva.

Dokaz:

Jasno je, za početak, da je svaki kvadrat po modulu kongruentan samo sa , ili ; prema tome, ukoliko se prirodan broj navedenog oblika može predstaviti kao zbir triju kvadrata, onda svaki od njih mora biti kongruentan sa po modulu , iz čega sledi da svaki mora biti neparan.

Dokažimo još da se svaki broj navedenog oblika zaista može predstaviti kao zbir triju kvadrata.

Pre svega, navešćemo stvari koje će nam trebati u dokazu.

• Dirihleova teorema. Svaki aritmetički niz čija je razlika uzajamno prosta s prvim članom sadrži beskonačno mnogo prostih brojeva.

— Dokaz ove teoreme je prilično komplikovan i verovatno nezanimljiv većem broju posetilaca ovog foruma. S druge strane, sama teorema je vrlo poznata i vrlo jednostavne formulacije, pa ju je sasvim opravdano koristiti bez dokaza.

• Osnovni pojmovi o celobrojnim (trinarnim) kvadratnim formama.

• Osnovni pojmovi o kvadratnim ostacima.

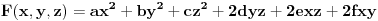
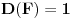
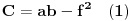
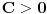
Neka je trinarna kvadratna forma takva da je . Označimo . Na osnovu Silvesterovog kriterijuma sledi da je pozitivno definitna akko je i (zapravo, ovo se jednostavno može dokazati i zasebno, ali dokaz je čista tehnikalija i nema realne potrebe za tim).

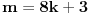
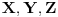
Da bismo dokazali teoremu, dovoljno je pokazati da za svako postoje trinarna kvadratna forma i vrednosti takvi da važi:





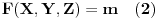
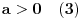
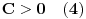
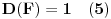
Evo jedne mogućnosti. Neka je:






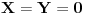
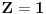
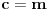
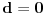
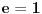
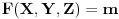
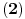
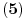
Primetimo da za ovako odabrane vrednosti važi , što ispunjava uslov . Uslov svodi se na:


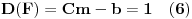
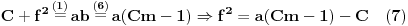
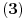
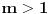
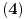
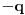
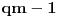
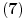
Sada imamo , što implicira uslov (svakako, ). Prema tome, dovoljno je za odabrati prirodan broj (ovim ispunjavamo uslov ) takav da je kvadrat po modulu , na osnovu čega ćemo iz dobiti .

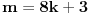
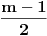
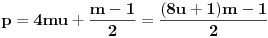
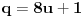
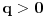
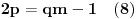
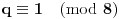
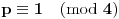
Kako je, podsetimo se, , zaključujemo da je neparan broj. Prema Dirihleovoj teoremi, postoji prost broj i prirodan broj takav da je . Odabraćemo . Tada je i . Sada iz i zaključujemo:


Takođe:
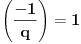
, jer je ;
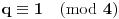
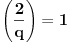
, jer je ;
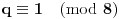
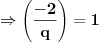
, jer su kvadratni ostaci multiplikativni.

Ovim je dokaz završen.

---

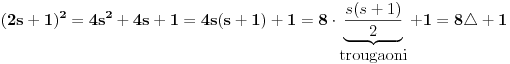
Preostaje još da se vidi kako ova teorema implicira tvrđenje zadatka. Zaista, primetimo da je . Prema tome, za svaki prirodan broj važi:

.
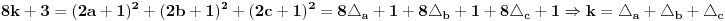