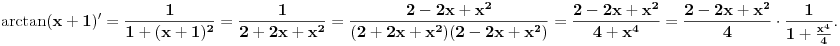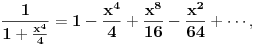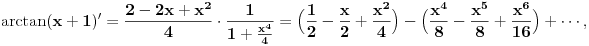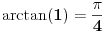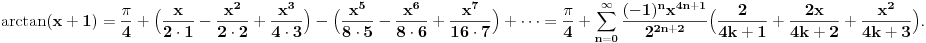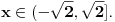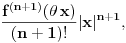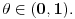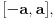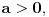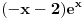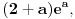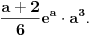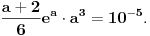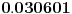[ solarko @ 15.01.2007. 18:09 ] @
| Poz! #1 Ako nije problem, zamolio bih nekog da mi pomogne oko Maklorenovog polinoma za f(x)=arctg(1+x) #2 Kako se radi sa Lagranzevim ostatakom? Recimo za gresku 10^-5, i Maklorenov 2 stepena od funkcije: (1-x)(e^x) Unapred zahvalan, solarko ------------------ Fakultet, a ne front ------------------ |