Treba da izracunas duzinu normale iz sredista stranice kocke na glavnu dijagonalu!

Ni ja ne mogu da shvatim sta se tacno trazi u zadatku :((. Tu se spominje GLAVNA dijagonala!?! Da li je to prostorna dijagonala kocke? Pretpostavljam da se na to misli. Evo ja sam poksao nacrtati to, sto se otprilike trazi, ali opet mi ne pada napamet ideja kako zadatak rijesiti. Koliko ja vidim, trebalo bi naci neku funkciju koja opisuje kako se mijenja "zelena duz", koja predstavlja rastojanje sredista strane kocke (tacka S) od dijagonale (u ovom slucaju dijagonala obojena u u narandzasto). To rastojanje se mijenja, a moguce je izracunati najmanje i najvece, ali to nije to.

[att_img]

Obicno se to rastojanje gleda kao normala na stranicu.. znaci ona linija koja ide kroz srediste da ma ugao 90° na stranicu.. znaci na tvojoj slici (ako gledas u 2d) ona zelena linija u sredini

ps. nisam siguran, ali ako bi ja to resavao, ja bi uzeo tu..

inace funkcija je obicna linearna (ako bi trebala funkcija)

Kao sto rekoh u prethodnom postu treba nam duzina normale iz sredista strane na glavnu dijagonalu!

D - glavna dijagonala
d - dijagonala strane kocke
a - stranica kocke
Pr -povrsina romboida
x - rastojanje koje trazimo

d = a*sqrt(2)
D = a*sqrt(3)
Sa jedne strane:
Pr = a*(d/2) = (a*a * sqrt(2)) / 2
a sa druge je:
Pr = D*x= a*sqrt(3)*x
I sada izjednacimo ovo:
(a*a*sqrt(2))/2 = a*sqrt(3)*x
pa je odavde:
x = a / sqrt(6)

Ako nisam negde pogresio u racunu :)

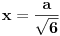
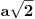
Ja sam isto dobio , samo sam radio na malo drugačiji način, preko sličnosti trouglova. Posmatrao sam pravougli trougao koji obrazuju jedna ivica kocke (), dijagonala susedne stranice () i glavna dijagonala ().

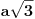
[att_img]

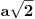
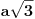
Kad iz središta katete () povučemo normalu na hipotenuzu (), dobićemo jedan manji trougao koji ima jednake uglove kao i veliki trougao, tako da možemo primeniti sličnost:

,

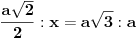
gde je tražena razdaljina.

_{[Ovu poruku je menjao Daniel011 dana 18.01.2007. u 01:51 GMT+1]}