[ Valerij Zajcev @ 24.01.2007. 12:55 ] @
|
| 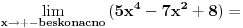
sada kada izvucem najveci stepen ispred zagrade zasto 7/x^2 tezi 0, isto i za 8/x^4 ??? I zasto je ovo +beskonacno |
[ Daniel011 @ 24.01.2007. 14:26 ] @
Pa što ti je u nekom razlomku veća vrednost imenioca, to ti je manja vrednost tog razlomka (tj. bliža nuli). Ne vidim šta te tu buni.
[ Valerij Zajcev @ 24.01.2007. 16:49 ] @
mm da da, resio sam problem, fora je valjda da x zamenim sa beskonacnim i to uvek tezi nuli. Bar sam to zakljucio iz gledanja po primerima.
[ Kolins Balaban @ 24.01.2007. 16:58 ] @
ovo ces jako cesto koristiti prilikom rjesavanja limesa:
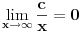
, gdje je c=const.
primjer
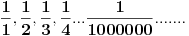
vidi se da se vrijednost razlomaka sve vise smanjuje. zadnji broj u nizu je jako mali, a koliko bi tek bio mali kad bi dodali jos 1000000000000000000000000 nula??? jelde da bi to bilo priblizno 0? ;)
kao i
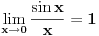
dok
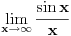
ne postoji
[ Bojan Basic @ 24.01.2007. 17:02 ] @
Postoji, i jednak je

.
[ Kolins Balaban @ 24.01.2007. 17:06 ] @
U pravu si bojane, pogrijesio sam.
Ovi limesi ne postoje:
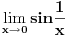
i
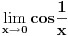
[ Batan @ 24.01.2007. 20:14 ] @
Da ne otvaram temu radi jednog primjera, zanima me sledece:
Imam lim (n -> beskonacno) 1 + 2 + 3 + ... + n / n^2
Da li je dovoljno da ovaj limes podijelim sa n^2 i da ga dovedem do kraja? ..ili nesto moram da radim vise, posto me ovo uvecavanje + .. + buni :( Hvala unaprijed!
[ Kolins Balaban @ 24.01.2007. 20:35 ] @
trebas da znas sljedece:
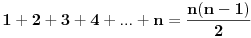
- lako se pokaze matematickom indukcijom, pa cu dokaz izostaviti.
Tvoj limes ima oblik
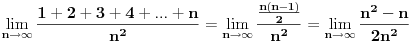
Nakon sto i brojnik i nazivnik podijelis sa
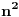
i pustis da
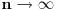
dobit ces da je
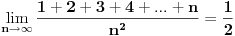
Eto, to je to valjda :)
[ Batan @ 24.01.2007. 20:46 ] @
A da.. nikako se sjetiti, a valjda treba n(n + 1) / 2
Hvala puno...
[ Daniel011 @ 24.01.2007. 20:49 ] @
Samo mala ispravka, formula za sumu aritmetičkog niza je
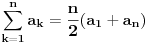
,
a za ovaj konkretan slučaj
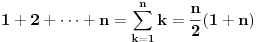
Rezultat je isti, tj. dobije se
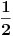
.
[ Kolins Balaban @ 24.01.2007. 20:55 ] @
da, lapsus, nisam ni vidio da sam - stavio, blizu tipke pa se pogrijesi :( al uglavnom, to je to, postupak je ok, a i rezultat :)
hvala na ispravkama ;)
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.