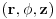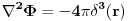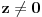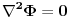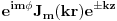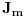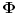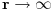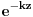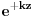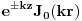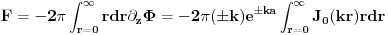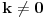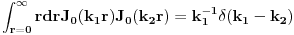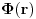Cini mi se da je odgovor na problem prost i proizilazi iz cinjenice da je fluks elektricnog polja kroz ravan paralelnu povrsini dielektrika koja se nalazi iznad naelektrisanja jednak po apsolutnoj vrednosti fluksu elektricnog polja kroz slicnu ravan koja se nalazi unutar dielektrika. Nazalost, nisam uspeo da nadjem elementaran nacin da ovo objasnim. Zato samo navodim sledece:

***********************************************************
Problem ima cilindricno simetriju oko ose koja prolazi kroz naelektrisanje i normalna je na povrsinu dielektrika.
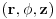
Stoga koristimo cilindricne koordinate gde z=0 odgovara lokaciji naelektrisanja a z=-d povrsini dielektrika.

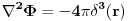
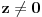
Jednacina koju resavamo, u cgs jedinicama, je . Za ovo postaje Laplace-ova jednacina .

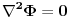
U homogenom prostoru bilo koje resenje Laplace-ove jednacine u cilindricnom koordinatama mozemo izraziti kao red pomocu kompletne baze resenja:
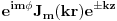
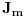
gde je Besselova funkcija m-tog reda.

Posto je problem aksijalno simetrican, ovde je potrebno koristiti samo m=0 funkcije.

U problemu imamo 3 homogena dela prostora: z>0, -d<z<0 i z<-d.
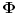
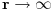
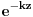
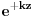
Dalje, posto je izvor polja ogranicen, ce biti konstantno kada . Zato za z>0 u razvitku potencijala u red koristimo samo a za z<-d samo funkcije.

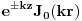
Sracunajmo sada fluks kroz ravan z=a:


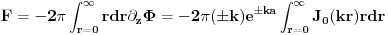
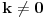
Medjutim, za , zadnji integral je 0. Razlog je ortogonalnost Besselovih funkcija (proizilazi iz Hermitian karaktera Besselove ODE):
.

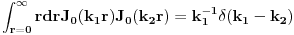
Zato fluks elektricnog polja parallelan z-osi nose samo komponente resenja sa infinitezimalno malim k. Posto te komponente prakticno ne zavise od z, one moraju imati istu amplitudu tj. koeficijent za z>0 i z<-d. To pak implicira da je fluks elektricnog polja na gore kroz ravan z=a>0 jednak fluksu elektricnog polja na dole kroz ravan z=b<-d. QED.
***********************************************************

Domaci1: koristeci gorenavedenu cinjenicu, resiti problem tj. naci vezano naelektrisanje na povrsini dielektrika.
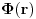
Domaci2: koristeci gorenavedenu bazu za razvijanje u red, naci u celom prostoru.