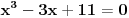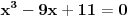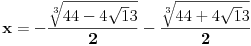[ Xarios @ 03.02.2007. 18:15 ] @
| pozdrav, Ako moze pomoc pri odredjivanju nule u sljedecoj funkciji: y= 1 + 3(x-2)2/(x-1)3 Evo dokle sam ja uradio: f(x)=0 => 1 + 3(x-2)2/(x-1)3 = 0 (x-1)3 + 3(x-2)2 = 0 x3-3x+11 = 0 . . Kako dalje i da li sam na dobrom putu??? Hvala unaprijed! |