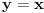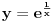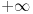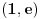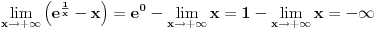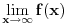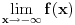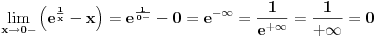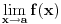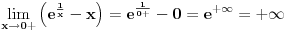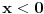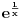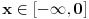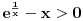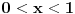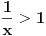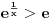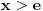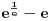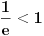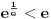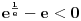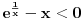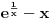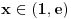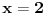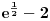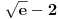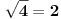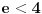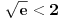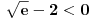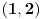Evo uradit cu dokle znam ''Nule i znak'':

y=0
e^1/x -x = 0
e^1/x = x (dobijemo x kad se prebaci s ljeve na desnu stranu)
to je to.
Ali ne znam kako se dobije X₀ je element intervala (1,2) ???

Isto tako ne znam kako se dobije sljedeca konstatacija: znak funkcije je + lijevo od nule, a - desno od nule. ???

Molim pomoc ...

I jedno i drugo možeš da vidiš ako nacrtaš u istom koordinatnom sistemu funkcije i .

Hint: sa leve strane y-ose od horizontalne asimptote koja prolazi kroz jedinicu uvire ka nuli,
a sa desne strane ima y-osu kao asimptotu i ide od do horizontalne asimptote. Prolazi kroz tačku .

U vezi asimptota:

- horizontalne asimptote:

=> nema horizontalnu asimptotu za , jer po definiciji horizontalna asimptota postoji ako i samo ako je konačan broj.

Ista priča važi i za .

- vertikalne asimptote:

=> nema vertikalnu asimptotu sa leve strane, jer po definiciji vertikalna asimptota u prekidnoj tački postoji ako i samo ako je beskonačan broj.

=> ima vertikalnu asimptotu sa desne strane.

Hvala Daniele,

sve mi je jasno, osim jedne sitnice: kao izraz 1 - lim_x->+ooX = - oo
odnosno kako se dobije -oo (minus beskonacno)???

je li mozda 1 - (+oo) = -oo ???

Upravo tako, Xarios. Evo primera:
1 - 1000 = -999
1 - 100000 = -99999
1 - 100000000000 = -99999999999
Dakle, što veći pozitivan broj oduzimamo od jedinice, to ćemo kao rezultat dobiti broj koji je sve bliži minus beskonačnosti.

Hvala puno Daniel.

Sto se tice nula funkcije, ne znam kao se izracuna i dobije X_o pripada (1,2) ??

Odnosno kako se dobije interval (1,2) od jednacine: e^1/x = x

Isto tako ne znam kako se dobije sljedeca konstatacija, racunanjem bez prvobitnog crtanja:
znak funkcije je + lijevo od nule, a - desno od nule. ???


ps:
za Kolins Balaban: poslao sam ti mail na tvoj privatni mail, od tada nisi komentirao na mojim postavljenim temama. Znam da nisi duzan to ciniti ali posto si prije to svojevoljno cinio, pomislio sam da se nisi nesto naljutio nakon mog maila kojeg sam poslao tebi.
Ukoliko jesi, iskreno se izvinjavam na mail-u.



_{[Ovu poruku je menjao Xarios dana 07.02.2007. u 18:50 GMT+1]}

Ako bih morao da određujem interval bez crtanja, išao bih ovim redom:

Za :
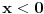
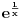
- je pozitivno, jer je to exponencijalna funkcija koja je uvek pozitivna bez obzira na znak exponenta;
- je negativno na osnovu uslova
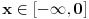
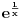
Prema, tome, za interval , mora biti veće od , tj. .

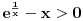
Za :
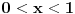
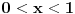
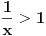
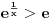
- pošto je , to znači da je , a to znači da je , a samim tim je veće i od (koje je po uslovu između i ), tako da opet važi da je .

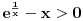
Za :
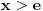
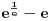
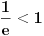
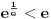
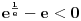
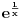
- za slučaj se svodi na ; tada, pošto je , biće i , tj. biće . Daljim povećavanjem , će sve više opadati, tako da će i daje važiti .

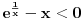
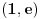
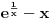
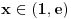
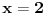
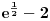
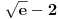
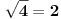
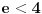
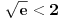
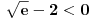
Ovime je pokazano da se nula nalazi u intervalu . Ako baš želiš da dodatno suziš ovaj interval, možeš da izračunaš izraz za neku vrednost , a najprirodnije je da ta vrednost bude 2, kao jedini ceo broj u ovom intervalu. Za , ovaj izraz bi se sveo na , tj. . Pošto je , a , znači da je , tj. . Znači, zaključujemo da nula mora da se nalazi u intervalu .

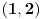
Sto se tice nule funkcije sada mi je jasno, ali ako se dobije znak funkcije: ''znak funkcije je + lijevo od nule, a - desno od nule''

jeli mozda ovako:

Upravo sam ti prethodnim postupkom objasnio i kako da lokalizuješ nulu funkcije, a i kako da odrediš gde funkcija ima znak +, a gde -. Verovatno nisi najpažljivije čitao.

Tvoja tabela je OK za x<0, tada su oba sabirka pozitivna pa će i zbir biti pozitivan, međutim kad je x>0, imaš dva sabirka suprotnog znaka, a da li će njihov zbir biti pozitivan ili negativan, zavisi od toga koji je sabirak veći po apsolutnoj vrednosti.

Sorry Xarios, nisam bas bio aktivan na forumu, jer sam imao nekih obaveza oko ispita itd. a i radio sam neku mrezicu u jednoj skoli. evo bas sam sada gledao privatne poruke, i tvoje uopste nema. ako si slao na moj mail, koji je naveden u profilu, njega vise ne koristim, jer se ukida na toj stranici (do sada je bio djabe, a sada traze da se placa taj servis, tako da ga ukidaju na stranici). ako ti treba pomoc, pisi mi ovdje na privat ;) pozz