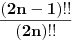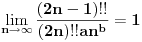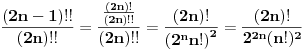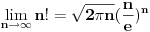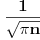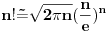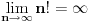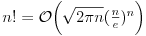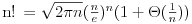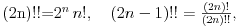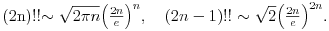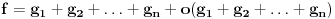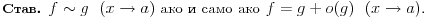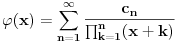[ darkosos @ 16.06.2003. 09:21 ] @
|
[ PeraT @ 22.06.2003. 01:25 ] @
Zar uopste postoje?
[ darkosos @ 22.06.2003. 08:31 ] @
Da. Nisam baš takav sadista da želim da se ljudi muče oko nečega što ne može :)
[ Mihailo Kolundzija @ 22.06.2003. 16:20 ] @
[ darkosos @ 22.06.2003. 17:56 ] @
[ Mihailo Kolundzija @ 22.06.2003. 19:44 ] @
Znam da nisam na odgovarajući način napisao, ali nije hteo lepo da mi prikaže "~" koju sam hteo na tom mestu da iskoristim umesto onog limesa.
[ darkosos @ 23.06.2003. 10:06 ] @
Ha, i ja sam imao isti problem; neće da prikaže ~ u tex modu.
Pokušaću da dobijem odgovor u tex-pitanjima. [ PeraT @ 29.06.2003. 01:13 ] @
Evo jos jednog glupog pitanja:
Kako se definise dvostruki faktorijal? Jel' faktorijal faktorijala ili nesto drugo? [ darkosos @ 29.06.2003. 10:33 ] @
Ma bre ovako :)
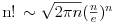 U prošlom post-u nisam znao da napišem samo ~ pa sam se kao snašao sa tildom nad znakom jednako. Koga interesuje, ~ se piše \sim (kao similar). Po izvorima koje ja imam, pravilno je f ~ g <=> f - g = o(g) kad x teži čemu već treba. Zbog simetrije verovatno može i o(f). To u stvari znači da je razlika zanemarljiva u odnosu na bilo koju od ove dve funkcije, tj. 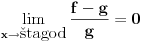 Tako da eventualno možemo pisati 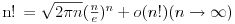 Možda ne bi bilo loše da se napravi top tema sa objašnjenjima za asimpotske relacije? Lepo se objasne o i O, i ostalo, kroz ekvivalentne zapise sa limesima. Mislim da je mnogima ova tema konfuzna. Mod: edit. [Ovu poruku je menjao filmil dana 29.06.2003. u 17:02 GMT] [ cedomir @ 29.06.2003. 12:05 ] @
Dvostruki faktorijel parnog broja je njegov proizvod sa svim parnim brojevima manjim od njega, a dvostruki faktorijel neparnog broja je njegov proizvod sa svim manjim neparnim brojevima.
[ Nedeljko @ 17.04.2004. 05:28 ] @
Koliko ja znam, Stirlingova formula za faktorijel bi trebala da glasi ovako: Postoji niz
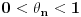 takav da za svako takav da za svako  važi važi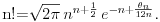 Što se tiče gama funkcije, za nju Stirlingova formula glasi: Postoji funkcija 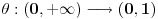 takva da za svako x>0 važi takva da za svako x>0 važi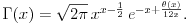 Često se u literaturi navodi da ove relacije važe počev odnekle, međutim tačan je i ovaj strožiji oblik. [ Nedeljko @ 17.04.2004. 05:41 ] @
[ Sonec @ 29.04.2012. 00:14 ] @
Jeste da je tema stara, al ne vidim da nesto fali ako se ponovo pokrene (bar se nadam da ce tako biti), naime, skoro smo radili Stirlinga; Gama, Beta, Vajerstrasovu, Rimanovu funkciju (steta sto nema neka tema za Gama funkciju, ona je bas interesantna, ima dosta razlicitih zapisa). Naime
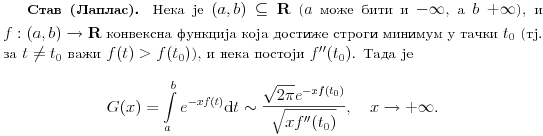 Pomocu ovog stava (koji uopste nije lak za dokaz (bar za mene (originalan Laplasov "dokaz" zasnivao se na rasudjivanju koje nije korektno, ali je dosta kraci od meni poznatog dokaza)) da se lako izvesti (ako nekoga zanima, mogu napisati) Stirlingova formula koja je data u nastavku teksta (posta, kako hocete) 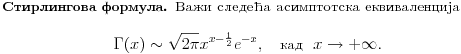 E sad, Nedeljko moze reci da je isto (bar meni izgleda da jeste) to i on rekao (mislim na Stirlinga). A evo sada mene interesuju Nedeljkove formule, i nacin na koji je tu asimptotska relaciija ~ zamenjena sa nizom, odnosno funkcijom (msm da se zna na sta ciljam). Taj deo mi nije najjasniji, pa ako moze neko objasnjenje bio bih zahvalan. malo sam vezbao  , izvinjavam se svima koji imaju probleme sa vidom, zbog sitnijeg fonta, nisam znao da to namestim , izvinjavam se svima koji imaju probleme sa vidom, zbog sitnijeg fonta, nisam znao da to namestima i konacno malo cirilice da vidim na ovom forumu [ darkosos @ 29.04.2012. 12:20 ] @
Iako nisam prozvan, svrativsi ovde, evo sta sam proceprkao http://cage.ugent.be/~ci/impens_stirling.pdf
Sto se tice "zamene aspimtotske relacije nizom" mislim da je to prica samo oko toga kako aproksimirati gresku koja se pravi... Slicno imas i kod Tejlorovog polinoma itd... [ Nedeljko @ 29.04.2012. 22:14 ] @
Sad je meni jasno šta pita sonec.
Neka je 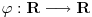 takve da je takve da je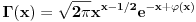 . .Rešavanjem ove jednakosti po 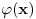 dobijamo da je dobijamo da je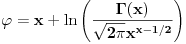 . .Odavde se direktno dobija da je 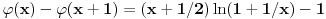 . .Ako hoćeš da potražiš asimptotski razvoj za 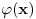 , tj. koeficijente , tj. koeficijente 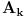 takve da je takve da je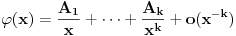 kada kada 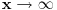 za te koeficijente mora da važi 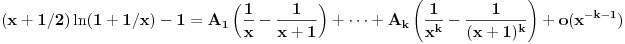 kada kada 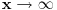 . .Dakle, razvijaj funkciju 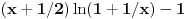 po funkcijama po funkcijama 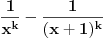 . .No, red 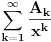 je divergentan. je divergentan.Konvergentan red ćeš dobiti ako potražiš funkciju 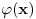 u obliku u obliku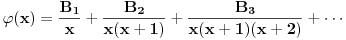 . .U tom slučaju mora da važi 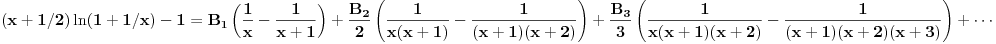 . .Konvergentan red[/url] ćeš dobiti ako potražiš funkciju 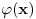 u obliku u obliku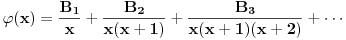 . .U tom slučaju mora da važi 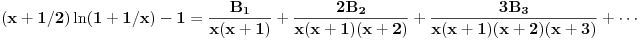 . .Dakle, razvijaj funkciju 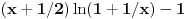 po funkcijama po funkcijama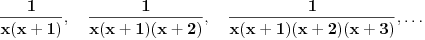 . .[Ovu poruku je menjao Nedeljko dana 30.04.2012. u 11:00 GMT+1] [ Sonec @ 30.04.2012. 00:27 ] @
Mene je interesovala veza (ako ona postoji) izmedju formula
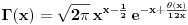 i i 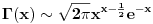 . Da li se iz jedne od ovih formula moze doci do druge? I uopste, da li postoji neka prica (ne vezano za Stirlinga) kako mozemo sa asimptotske relacije da predjemo na nesto sto je aproksimirano sa nizom ili pak funkcijom (kako je ovde ucinjeno)? . Da li se iz jedne od ovih formula moze doci do druge? I uopste, da li postoji neka prica (ne vezano za Stirlinga) kako mozemo sa asimptotske relacije da predjemo na nesto sto je aproksimirano sa nizom ili pak funkcijom (kako je ovde ucinjeno)?Nije mi poznat pojam "Asimptotskog razvoja" (moram priznati), pogledao sam malo na internetu i u sustini sam video sta je filozofija. Ja sam formulu 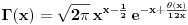 nasao kod Kadelburga (ali, bez dokaza), gde je receno da se dokaz moze naci kod nasao kod Kadelburga (ali, bez dokaza), gde je receno da se dokaz moze naci kod Code: gde se mogao naci dokaz za formulu Matematičeskiй analiz (V.A. Ilьin, V.A. Sadovničiй, Bl.H. Sendov), 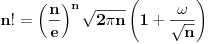 , gde , gde  . .Zatim je data napomena, da se moze pokazati 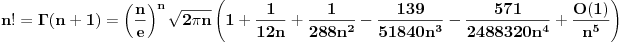 (sto doduse pise i na wikipediji), i da se to moze naci kod (sto doduse pise i na wikipediji), i da se to moze naci kodCode: Osnovы matematičeskogo analiza. V 2-h č. Ilьin V.A., Poznяk Э.G. Tako da sam video ono sto me je zanimalo. I hvala na trudu obojici. nema potrebe da se odgovara na gornja pitanja (sem ako bas ne zelite), ne znam ni sto sam ih postavio (al neka stoje tu, necu ih brisati) [ darkosos @ 30.04.2012. 09:04 ] @
Citat: Sonec: Mene je interesovala veza (ako ona postoji) izmedju formula 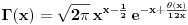 i i 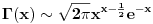 . Da li se iz jedne od ovih formula moze doci do druge? I uopste, da li postoji neka prica (ne vezano za Stirlinga) kako mozemo sa asimptotske relacije da predjemo na nesto sto je aproksimirano sa nizom ili pak funkcijom (kako je ovde ucinjeno)? . Da li se iz jedne od ovih formula moze doci do druge? I uopste, da li postoji neka prica (ne vezano za Stirlinga) kako mozemo sa asimptotske relacije da predjemo na nesto sto je aproksimirano sa nizom ili pak funkcijom (kako je ovde ucinjeno)?Rekao bih da tu nema niceg specijalnog, onaj dodatak niza je samo malo bolja aproksimacija. Zamisli da dodas jos jedan clan na Tejlorov polinom, ili u ovom slucaju, na asimptotski razvoj. Dakle nema tu nekog "izvodjenja", osim sto mozes da kazes da je druga formula posledica prva, tj neka vrsta skracene verzije. Dakle, npr imas as. razvoj f = g1 + g2 + ... + o(gn). Oblik kao sto je prva formula, dobijes kad o(gn) zamenis funkcijom odgovarajucih osobina. A oblik kao sto je druga formula se dobije tako sto se prosto zapise f ~ g1 + g2 + ... + gn. [ Sonec @ 30.04.2012. 12:07 ] @
[ darkosos @ 30.04.2012. 12:31 ] @
Da, zaboravio sam da napisem taj clan :) Ali inace je o(gn) jer je sam razvoj napravljen tako... To sto si ti napisao je primenjena definicija u opstem slucaju...
[ Nedeljko @ 30.04.2012. 14:32 ] @
Razvi funkciju
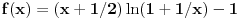 u red u okolini beskonačnosti. Ako ti nije jasno šta to znači, ti uvedi smenu u red u okolini beskonačnosti. Ako ti nije jasno šta to znači, ti uvedi smenu 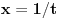 , pa razvijaj u okolini nule. Dobićeš sledeće , pa razvijaj u okolini nule. Dobićeš sledeće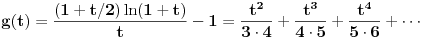 . .E, sad, ovo nećeš razvijati u red po funkcijama 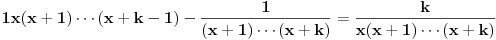 , , 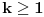 već zbog uvedene smene po funkcijama 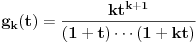 . .Najpre nađi koeficijent  takav da je takav da je 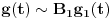 kad kad 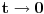 . Zatim nađi koeficijent . Zatim nađi koeficijent 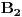 takav da je takav da je 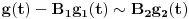 kad kad 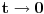 . .Drugim rečima, neka je 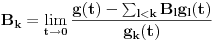 . .Za tako definisane koeficijente važi  za za 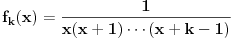 . .Štaviše,  , tj. taj red konvergira ka , tj. taj red konvergira ka  . .[ Sonec @ 01.05.2012. 23:22 ] @
Citat: Da, provera, 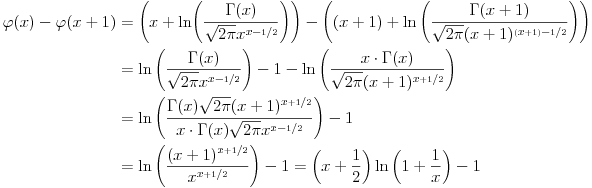 Citat: Nedeljko: Razvi funkciju 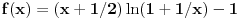 u red u okolini beskonačnosti. Ako ti nije jasno šta to znači, ti uvedi smenu u red u okolini beskonačnosti. Ako ti nije jasno šta to znači, ti uvedi smenu 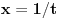 , pa razvijaj u okolini nule. Dobićeš sledeće , pa razvijaj u okolini nule. Dobićeš sledeće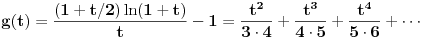 . .Ja sam dobio drugacije, naime, 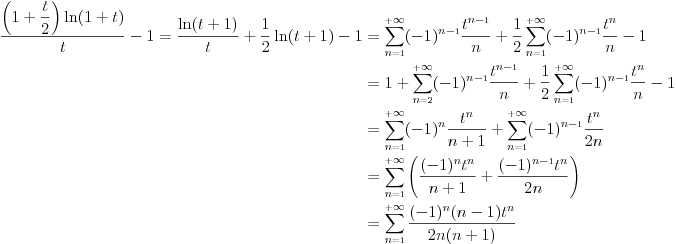 Odnosno,  Inace, kako bi se razvila ova funkcija direktno u red u okolini beskonacnosti? [mozda ja nemam jos dovoljno znanja za tu metodu, ne znam] Citat: Ovde te je prevario 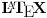 , ali znam na sta si mislio. , ali znam na sta si mislio.Citat: Nedeljko: Najpre nađi koeficijent 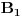 takav da je takav da je 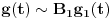 kad kad 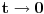 . Zatim nađi koeficijent . Zatim nađi koeficijent 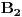 takav da je takav da je 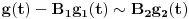 kad kad 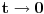 . .Drugim rečima, neka je 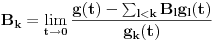 . .Ovaj deo razumem. Citat: Ovde si ti vratio smenu (koliko ja vidim), al zasto definises 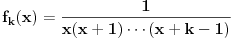 , zar nije , zar nije  ? Gde gresim? Ili se ovo odnosi na to kad si mi rekao da razvijem funkciju ? Gde gresim? Ili se ovo odnosi na to kad si mi rekao da razvijem funkciju  po po 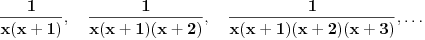 ? (ali, i dalje stoji da ? (ali, i dalje stoji da 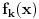 bi trebalo drugacije definisati, il ja gresim ko sto rekoh) bi trebalo drugacije definisati, il ja gresim ko sto rekoh) Citat: Jel ovo neki poznat rezultat ili se lako vidi iz tvog posta (posto ja ne vidim (sto ne znaci da nema))? ___________________________________________________ I sad na kraju, najvaznije pitanje, sta ti meni pokusavas da pokazes? Nije mi jasno na sta ciljas. [ Nedeljko @ 02.05.2012. 00:41 ] @
Odakle funkcija
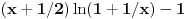 ? Pa, ? Pa,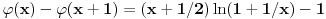 . .Ako je 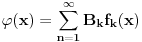 , koliko je , koliko je 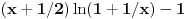 ? Koliko je ? Koliko je 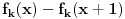 ? Da nije možda ? Da nije možda 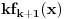 ? ?Što se ratvoja funkcije 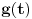 tiče, dobar ti je, ja sam pogrešio. tiče, dobar ti je, ja sam pogrešio.Što se tiče konvergencije, važi sledeće: Funkcija 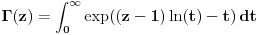 , za , za 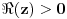 je analitička (na navedenom domenu) jer je granična vrednost lokalno ravnomerno konvergentnog niza analitičkih funkcija. Na primer, je analitička (na navedenom domenu) jer je granična vrednost lokalno ravnomerno konvergentnog niza analitičkih funkcija. Na primer,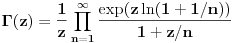 . .Štaviše, gama funkcija je analitička u celoj kompleksnoj ravni bez nepozitivnih celih tačaka. Stoga njen Tejlorov razvoj u okolini tačke  , , 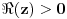 konvergira na otvorenom disku poluprečnika konvergira na otvorenom disku poluprečnika  (pa i više, na disku poluprečnika (pa i više, na disku poluprečnika 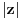 ). Otuda je i realna varijanta gama funkcije analitička na intervalu ). Otuda je i realna varijanta gama funkcije analitička na intervalu 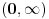 . .Koeficijenti 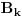 se mogu izraziti preko Stirlingovih brojeva, koji su dobro proučeni, pa se na osnovu njihove procene može dokazati (valjda, nisam računao, ali tako bih probao) da je pomenuti red lokalno ravnomerno konvergentan (u kompleksnoj poluravni desno od imaginarne ose), pa pošto su svi članovi analitičke funkcije i suma je analitička funkcija. se mogu izraziti preko Stirlingovih brojeva, koji su dobro proučeni, pa se na osnovu njihove procene može dokazati (valjda, nisam računao, ali tako bih probao) da je pomenuti red lokalno ravnomerno konvergentan (u kompleksnoj poluravni desno od imaginarne ose), pa pošto su svi članovi analitičke funkcije i suma je analitička funkcija.Nakon toga uvedi smenu 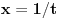 . Zajedno sa funkcijom . Zajedno sa funkcijom 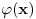 , funkcija , funkcija  je meromorfna sa otklonjivim singularitetom u nuli (upravo po Stirlingovoj formuli je je meromorfna sa otklonjivim singularitetom u nuli (upravo po Stirlingovoj formuli je  ). Dakle, treba dokazati da je ). Dakle, treba dokazati da je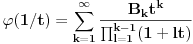 , ,pri čemu opet imamo posla sa jednakošću dveju analitičkih funkcija. Dovoljno je dokazati da imaju jednake Maklorinove razvoje. No, to sledi iz činjenice da za 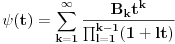 važi važi . .Ovako bih ja pokušao da dokažem. [ Sonec @ 02.05.2012. 09:43 ] @
Citat: Pa da, to sam i rekao u mom prethodnom postu, tacnije, napisao sam racun, tj. proverio tvoj racun. _______________________________________________________________________________ Ja ne znam Kompleksnu Analizu, taj predmet cu slusati iduce godine. Verovatno cu se iduce godine smejati koliko je ovo "lako", ali za sada to su za mene nepoznati pojmovi. Da li to bas mora preko kompleksne ili ti pak pokusavas da me zaplasis, ja ne znam. Zapamticu ovu pricu, pa cu se vratiti na nju iduce godine, kad sve malo bolje proucim. Hvala na trudu, nekome ce znaciti verujem. [ Nedeljko @ 02.05.2012. 10:44 ] @
Ma, ne pokušavam ja nikoga da plašim. Nemam pojma kako se ta teorema standardno dokazuje. Nikada nisam video nijedan dokaz, pa sam napisao skicu kako bih ja to dokazivao. Da probam drugačije.
Na osnovu procene apsolutne vrednosti Stirlingovih brojeva se može proceniti apsolutna vrednost koeficijenata 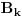 i onda dokazati da red i onda dokazati da red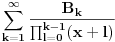 ravnomerno konvergira na 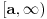 za za  . Samim tim možemo govoriti o njegovoj sumi . Samim tim možemo govoriti o njegovoj sumi 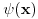 kao neprekidnoj funkciji. kao neprekidnoj funkciji.Koeficijenti 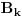 su taman takvi da je su taman takvi da je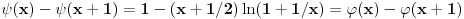 . .Po Stirlingovoj formuli je  , a na osnovu pomenute ravnomerne konvergencije je , a na osnovu pomenute ravnomerne konvergencije je 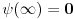 . Stoga je . Stoga je , , . .Puštajući da 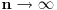 dobijamo da je dobijamo da je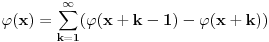 , ,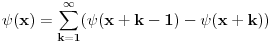 . .Iz 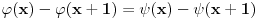 i prethodnih relacija napokon sledi da je i prethodnih relacija napokon sledi da je  . .Je li sada lakše? Napominjem da procenu apsolutne vrednosti Stirlingovih brojeva nisam radio, tako da to treba proveriti. [ Nedeljko @ 02.05.2012. 13:04 ] @
Ovo pišem zato što si pitao zašto važi onaj razvoj. Inače, ove stvari možeš naći na vikipediji.
Zapravo, treba da bude  , pa funkciju , pa funkciju treba potražiti u obliku  . .E, sad, dokazuje se da je 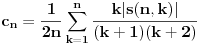 . .Obzirom na definiciju Stirlingovih brojeva preko  važi 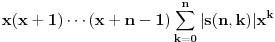 . .Zamenom  sa 1 zaključuje s da je sa 1 zaključuje s da je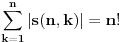 , ,pa važi 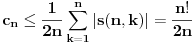 . .Sada možemo proceniti opšti član našeg reda.  . .Odavde na osnovu poredbenog kriterijuma dobijamo apsolutnu konvergenciju našeg reda za svako 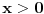 . Ostalo je da se dokaže ravnomerna konvergencija na . Ostalo je da se dokaže ravnomerna konvergencija na 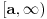 za bilo koje za bilo koje  . To sledi iz prethodno dokazane konvergencije reda i činjenice da mu je opšti član pozitivna opadajuća funkcija po . To sledi iz prethodno dokazane konvergencije reda i činjenice da mu je opšti član pozitivna opadajuća funkcija po  . .[Ovu poruku je menjao Nedeljko dana 02.05.2012. u 14:57 GMT+1] [ Nedeljko @ 02.05.2012. 20:28 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|