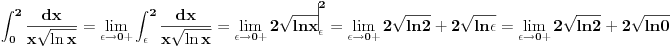[ simb @ 21.02.2007. 21:48 ] @
|
[ Daniel011 @ 22.02.2007. 05:41 ] @
Koliko ja vidim, problematične su granice integrala, jer funkcija
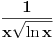 nije definisana na celom tom intervalu. nije definisana na celom tom intervalu.Da bi ta funkcija bila definisana, mora biti zadovoljeno:  , ,tj. kad se objedine svi ovi uslovi, 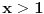 . .Znači, za 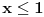 funkcija funkcija 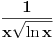 nije definisana, pa se ni njen integral ne može tražiti u opsegu od 0 do 1. nije definisana, pa se ni njen integral ne može tražiti u opsegu od 0 do 1.A inače bi se ovaj integral, kao neodređen, mogao rešiti na dva načina, jedan je uvođenjem smene 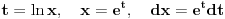 , a drugi način je da se , a drugi način je da se 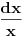 napiše kao napiše kao 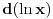 . Rešenje bi bilo . Rešenje bi bilo 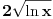 . .[ simb @ 22.02.2007. 09:29 ] @
Citat: Daniel011: Koliko ja vidim, problematične su granice integrala, jer funkcija 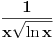 nije definisana na celom tom intervalu. nije definisana na celom tom intervalu.U tome i jeste problem, u pitanju je nesvojstveni integral. Kada sam ga rješavao kao neodređeni dobio sam isti rezultat. Ali sa nesvojstvenim integralima se nisam prije sustretao. Hvala u svakom slučaju za trud. Ima li možda neko nekakvu literaturu ili primjere kako se rješavaju nesvojstveni integrali prve i druge vrste? [ Djurdjica Djurdjevic @ 03.03.2007. 18:50 ] @
Def:
Neka je funkcija f DEFINISANA u intervalu [a,b) i integrabilna na svakom segmentu [a, beta) << [a,b) Ako postoji limes lim(kad beta-> b-0) INTEGRAL(od a do beta) f(x)dx on se naziva nesvojstvenim integralom funkcije f na intervalu [a,b) i oznacava sa INTEGRAL(od a do b) f(x)dx. ( slicno moze i alfa da tezi ka a) U tvom primeru: Ako se uzme limes(kad alfa->0) INTEGRAL(od alfa do 2) f(x) dx dobija se nakon smene lnx=t, da je taj limes ne postoji. Izvinjavam se na ruznom izgledu poruke. [ Nedeljko @ 11.03.2007. 11:45 ] @
Ne, nije, jer podintegralna funkcija mora da bude definisana svuda na domenu integracija, osim, eventualno, na diskretnom skupu tačaka da bi se uopšte moglo govoriti o nesvojstvenom integralu. Drugim rečima, to što si postavci napisao nije nesvojstveni integral.
[ simb @ 11.03.2007. 14:26 ] @
Ali u postavci zadatka piše izračunati nesvojstveni integral!?
[ mickey6252 @ 11.03.2007. 23:23 ] @
Citat: simb: Ali u postavci zadatka piše izračunati nesvojstveni integral!? :) A ti napiši da ćeš izračunati onda kada ti oni postave nesvojstveni integral, jer ovo jednostavno nije nesvojstveni integral. [ simb @ 12.03.2007. 20:02 ] @
[ Neznalica_sa_ugla @ 15.03.2007. 14:32 ] @
u ovom slucaju radi se o greški . treba stajati od 1 do 2 i onda ovaj vaš postupak bi bio ok. Autor knjige je i objavio ispravke u prilogu ispravka , jednog od izdanja.
[ simb @ 15.03.2007. 21:31 ] @
OK, hvala svima koji su mi pomogli da riješim ovu misteriju.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|