[ petarm @ 25.02.2007. 11:33 ] @
| U ovoj temi trebalo bi da navedete vama najlepsi (najlepse) dokaze u matematici. I da ih ispisete. Moglo bi da bude veoma interesantno. |
|
[ petarm @ 25.02.2007. 11:33 ] @
[ boxxter @ 09.07.2010. 00:08 ] @
„Gedelov dokaz“ sastoji se zapravo od dve teoreme. U prvoj se dokazuje da je nekompletna bilo koja teorija koja uključuje prirodne brojeve (1, 2, 3, 4, ... ). U drugoj teoremi Gedel tvrdi da se takve teorije ne mogu dokazati unutar istog sistema aksioma. Za dokazivanja ovakvih teorema polazni aksiomi su nedovoljni, potrebno je izaći u neki veći sistem aksioma. Ali, dokazivanje u većoj teoriji takođe zahteva jos veću teoriju – i tako u nedogled.
Njegova teorema kaze da je u nekim slučajevima nemoguće naći dovoljno aksioma da bi moglo da se odgovori na sva pitanja. Matematičko saznanje predodređeno je da zauvek ostane delimično nepotpuno (nekompletno). Zato se njegova teorema izvorno zvala „teoreme nekompletnosti“. Čak i gore od toga, on je pokazao da je jedno od pitanja na koje ne može da se odgovori i to da li je izabrana grupa aksioma za neki dokaz pravilno odabrana ili se u njoj krije neka protivrečnost. Pre Gedelove teoreme svi su verovali da je matematika, vazna alatka prirodnih nauka, jedina nauka koja može da pruži apsolutnu istinu i da je matematički postupak jedini put do savršenog saznanja. Na neki način, to i jeste tako. Pitagorina teorema vazi i danas u nepromenjenom obliku kakav je imala pre 3000 godina i takva će ostati. Suprotno drugim naukama, gde se teorije vremenom menjaju ili čak odbacuju, kad matematika jednom utvrdi da je nešto tačno, to zauvek ostaje tako. Gedel je, u stvari, otkrio da ni matematika nije savršena nauka i da nije imuna na pitanja na koja ne može tačno da odgovori. Njihova tačnost samo je pitanje uverenja. Gedelova teorema ne tvrdi da je sama matematika nepotpuna, već svaki sistem koji pokušava da obuhvata sve istine u matematici u vidu konačnog skupa aksioma i pravila. Međutim, za vodeće matematičare iz tridesetih godina proslog veka i ovo saznanje je bilo pravi šok jer je oborilo njihovo poimanje matematike i sveta. Gedelov tekst iz 1931. godine proizveo je još nešto: teoriju takozvanih rekurzivnih funkcija koje su danas osnova moćne računske teorije. Jer u srži njegovog rada bio je računski program za proizvodnju M. P. brojeva, na koji veoma podseća programski jezik Lisp, osmišljen skoro tri decenije kasnije. Gedelova teorema o potpunosti je teorema matematičke logike koju je dokazao Kurt Gedel u svojoj doktorskoj disertaciji 1929. i kasnije u radu objavljenom 1930. U svom najpoznatijem obliku, ona tvrdi da je u predikatskom računu prvog reda svaka logički valjana formula dokaziva. Ovo je jedna od najvažnijih teorema matematičke logike, jer pokazuje da klasičan predikatski račun "sadrži" sve zakone logike koji se mogu iskazati predikatskim formulama. Gedelova teorema o potpunosti u osnovi glasi: Citat: Postoji račun predikatske logike prvog reda takav da za svaki skup formula Γ i svaku formulu φ važi: φ sledi iz Γ ako i samo ako se φ može izvesti iz Γ u ovom računu U matematičkoj logici, Gedelove teoreme o nepotpunosti su dve čuvene teoreme o ograničenjima formalnog sistema, koje je dokazao Kurt Gedel, 1931 godine. Gedelova prva teorema o nepotpunosti je verovatno najslavniji rezultat u matematičkoj logici. Ona tvrdi da: Citat: Za bilo koju formalnu teoriju koja potvrđuje osnovne aritmetičke istine, može se konstruisati aritmetičko tvrđenje koje je istinito ali nije i dokazivo unutar same te teorije. To znači, da bilo koja teorija koja je sposobna da izrazi elementarnu aritmetiku ne može biti u isto vreme i konzistentna i potpuna. Dokaz =) Zamislimo da se na nekoj udaljenoj planeti (Marsu, na primer), takođe pišu udzbenici matematike. Pretpostavimo da, nekom čudnom slučajnošću, svi simboli koje Marsovci koriste da bi napisali matematičke knjige izgledaju kao naši brojevi od 0 do 9. Zato kada Marsovci u svojim udzbenicima razmateraju neko od čuvenih otkrića, recimo aksiom koji mi pripisujemo Euklidu i koji glasi : „Postoji beskonačno mnogo prostih brojeva“, oni ga mozda iskazuju ovako : 84453298445302152010024887950234. Ono što nama izgleda kao jedan veliki tridesetdvocifreni broj, za Marsovce uopšte nije broj, nego iskaz. On Marsovcima govori da postoji beskonačnost prostih brojeva, isto tako jasno kao i nama pomenutih pet reči. Sada zamislimo da želimo da pričamo o prirodi svih matematičkih teorema. Ako pogledamo u marsovske udzbenike, sve te teoreme izgledaće nam kao brojevi. Znači da možemo da razvijemo i jednu podrobnu teoriju o tome koji brojevi mogu da se pojave u marsovskim udzbenicima, a koji se nikada neće pojaviti. Naravno, ne mora doslovno da se radi o našim brojevima, već o nizu simbola koji nama izgledaju kao brojevi. Na temelju ovako izokrenutog gledišta Gedel je izgradio pravu čaroliju. Njegov trik sastoji se u tome da sada zamislimo da u marsovskim udzbenicima proučavamo brojeve koji zu zapravo teoreme. Nazovimo ih skraćeno „M. P.“ brojevima (od Martian – Producible numbers). Onda možemo da postavimo pitanja : „da li je neki broj 8030974, M. P. broj, ili nije? To jest, da li će izraz 8030974 ikada da se pojavi u marsovskim udzbenicima matematike jer je teorema? Razmišljajući veoma pažljivo o ovom sasvim nerealnom scenariju, Gedel je shvatio da se osobine M. P. brojeva ne razlikuju od tako uobičajenih predstava kao što su „prost broj“, „neparan broj“ i tako dalje. To je značilo da zemaljski teoretičari, koristeći svoje uobičajene postupke, mogu da razmatraju i takva pitanja kao što je „Koji brojevi su M. P. brojevi, a koji nisu?“ i slično. I tako, u jednom od najoštroumnijjih zaključivanja u istoriji matematike, Gedel je osmislio izvanredan iskaz koji jednostavno glasi : „X nije M. P. broj“, gde je X broj koji vidimo kada je izraz „X nije M. P. broj“ preveden na marsovski matematički jezik. Kada se izraz „X nije M. P. broj“ prevede na marsovski sistem znakova izgledaće nam samo kao dugački niz cifara, to jest, vrlo veliki broj. Ali taj niz marsovskih znakova je i naš zapis za broj X, o kome i sam iskaz govori. Ovo znači da nije moguće potvrditi tačnost iskaza u datom sistemu. =) Gedelov rad ostavio je dubok trag ne samo u matematici. Čitavog života beležio je svoje matematičke misli. Neki od njegovih radova toliko su složeni da se veruje da će proći vekovi pre nego što se odgonetnu, potvrde ili ospore. Pre njega matematičari, kao uostalom i naučnici u nekim drugim oblastima, smatrali su da stoje na samim vratima konačne istine. Gedel je doneo otrežnjenje: pokazao je da nismo Bogovi, već samo ljudska bića sa ograničenim saznajnim mogućnostima. [ boxxter @ 10.07.2010. 10:55 ] @
1+1=2
Principia Mathematica  [ boxxter @ 10.07.2010. 11:04 ] @
Russell-ov paradoks.
Assuming RUSSELL∈RUSSELL leads to a contradiction for, by definition, RUSSELL does not contain itself. Assuming RUSSELL∉RUSSELL implies that RUSSELL satisfies the definition and, hence, RUSSELL∈RUSSELL. Impossibility. That RUSSELL is such a set that neither RUSSELL∈RUSSELL nor RUSSELL∉RUSSELL has been discovered by Bertrand Russell (1872-1970) in 1901. This is how he described the event in his Autobiography: At the end of the Lent Term, Alys and I went back to Femhurst, where I set to work to write out the logical deduction of mathematics which afterwards became Principia Mathematica. I thought the work was nearly finished, but in the month of May I had an intellectual set-back almost as severe as the emotional set-back which I had had in February. Cantor had a proof that there is no greatest number, and it seemed to me that the number of all the things in the world ought to be the greatest possible. Accordingly, I examined his proof with some minuteness, and endeavoured to apply it to the class of all the things there are. This led me to consider those classes which are not members of themselves, and to ask whether the class of such classes is or is not a member of itself. I found that either answer implies its contradictory. At first I supposed that I should be able to overcome the contradiction quite easily, and that probably there was some trivial error in the reasoning. Gradually, however, it became clear that this was not the case. Burali-Forti had already discovered a similar contradiction, and it turned out on logical analysis that there was an affinity with the ancient Greek contradiction about Epimenides the Cretan, who said that all Cretans are liars. A contradiction essentially similar to that of Epimenides can be created by giving a person a piece of paper on which is written: 'The statement on the other side of this paper is false.' The person turns the paper over, and finds on the other side: 'The statement on the other side of this paper is true.' It seemed unworthy of a grown man to spend his time on such trivialities, but what was I to do? =) There was something wrong, since such contradictions were unavoidable on ordinary premises. Trivial or not, the matter was a challenge. Throughout the latter half of 1901 I supposed the solution would be easy, but by the end of that time I had concluded that it was a big job. I therefore decided to finish The Principles of Mathematics, leaving the solution in abeyance. In the autumn Alys and I went back to Cambridge, as I had been invited to give two terms' lectures on mathematical logic. These lectures contained the outline of Principia Mathematica, but without any method of dealing with the contradictions. Principia Mathematica is the book Russell wrote with Alfred North Whitehead where they gave a logical foundation of Mathematics by developing the Theory of Types that obviated the Russell's paradox. This assertion may become more convincing after a look at the page 362 of Principia Mathematica where Russell and Whitehead finally proved that 1 + 1 = 2. [ boxxter @ 10.07.2010. 11:15 ] @
The University of Michigan Historical Mathematics Collection
http://quod.lib.umich.edu/u/umhistmath/ http://quod.lib.umich.edu/cgi/...age;seq=126;page=root;size=100  [ boxxter @ 10.07.2010. 11:28 ] @
Bonus: =)
Poincaré nije voleo Peanov rad na formalnom jeziku matematike, tada zvanim logistickim. Napisao je o Russell-ovom paradoksu, sa ociglednim zadovoljstvom, " Logistika je konacno dokazala da nije sterilna. Napokon je rodila - kontradikciju. :) R.Hersh, Sta je matematika u stvari? Oxford University Press, 1997 [ boxxter @ 10.07.2010. 16:31 ] @
Teorija cvora
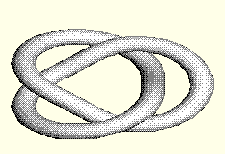 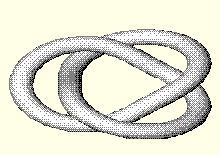 Gore je slika levog trolistog cvora. A ispod njega je slika desnog trolistog cvora. Nemoguce je da se razvlacenjem i uvrtanjem, ali ne izazvavsi neko ostecenje ili prekid, pretvori jednog u drugi. Kako god, moramo da primetimo, da su ova dva cvora topoloski jednaki u smislu da postoji topoloska transformacija koja ih mapira u jednog u drugi. Cvorovi su odraz u ogledalu, jednog, od drugog. U realnom svetu, mozemo da vodimo raspravu o tome da su odrazi u ogledalu samo mentalne slike cije je postojanje potpuno drugacije od objekta ciji su odraz. U matematici, odrazi su stvarni kao i sami objekti. Matematicki, odrazi su topoloske transformacije, koje se ne mogu prevesti na objekte iz stvarnosti. Ali kao sto mnogi matematicari govore, nijedna matematicka transformacija se ne moze prevesti na obekte iz stvarnosti. Interesantno je u trigonometriji i analitickoj geometriji provaliti skup jednacina kojima rezultiraju ove slike. U teoriji cvora do 1984 glavni alat za razumevanje cvorova su bili aleksanderovi polinomi. Ali oni nisu pravili razliku izmedju dva cvora. Za oba cvora Aleksandrovi polinomi su bili 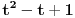 . 1984-te, Zealander Vaughan Jones je radio na nekim aspektima matematicke fizike i otkrio polinome, koju su kasnije razvijene simultano i nezavisno do strane pet razlicitih grupa matematicara. Poznati kao HOMFLY (Hoste-Ocneanu-Millett-Freyd-Lickorish-Yetter), ovi polinomi u dve varijante daju . 1984-te, Zealander Vaughan Jones je radio na nekim aspektima matematicke fizike i otkrio polinome, koju su kasnije razvijene simultano i nezavisno do strane pet razlicitih grupa matematicara. Poznati kao HOMFLY (Hoste-Ocneanu-Millett-Freyd-Lickorish-Yetter), ovi polinomi u dve varijante daju 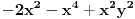 za levi, i za levi, i 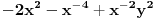 za desni cvor, respektivno. za desni cvor, respektivno.Kraj filozofskoj diskusiji, da li je matematika izmisljena, ili otkrivena, nije nigde na vidiku. [Ovu poruku je menjao boxxter dana 10.07.2010. u 17:41 GMT+1] [Ovu poruku je menjao boxxter dana 10.07.2010. u 17:42 GMT+1] [ boxxter @ 10.07.2010. 16:56 ] @
Krajem 18. veka, u vreme kada se još nije znalo za periodni sistem elemenata, naučnici su, kao i uvek, pokušavali da razumeju osnovno ustrojstvo sveta. Konkretno, Tompson je smatrao da se elektromagnetski talasi, tada tek otkriveni, kreću kroz etar u vrtloznim putanjama, nalik na čvorove.
Oni, i drugi, su razvili čitavu taksonomiju čvorova, misleći da time mogu da opisu raznovrsnost prirode, da na taj način prave neku vrstu tablice molekula. Naravno, sa pojavom Mendeljejevog sistema, ova teorija je odbačena i bila je neko vreme sasvim zaboravljena. Medjutim, tokom prve četvrtine 20. veka, matematičari su počeli da pokazuju interes za čvorove, posebno za njihove topološke osobine. Najvazniji prodor u tom pravcu pravi J.W. Aleksander, čuveni topology, i jedan od prvih članova prinstonskog Instituta za Više Studije, na kome je pred kraj zivota radio Ajnstajn i mnogi drugi poznati fizičari 20. veka. Aleksander je uspeo 1924. da klasifikuje čvorove na algebarski način, uvodeći tzv. Aleksandrove polinome. Naime, svakom čvoru moze da se pridruzi karakterističan algebarski izraz, polinomskog oblika, pa dva čvora koja imaju isti pridruzen polinom (Aleksandrov polinom) morali bi da budu toploški ekvivalentni. Konkretno, najprostiji čvor u matematici je obična kruzna petlja kao na slici:  Ova dva čvora su ekvivalentna jedan drugom u topološkom smislu, jer se jedan moze tansformisati u drugi neprekidnim deformacijama (bez korišćenja makaza, na primer). Ovaj osnovni čvor se zove nečvor. Čvor, u matematici, se dobija tako što se veze običan čvor, kao sto bi to "normalno" uradili, i onda mu se slobodni krajevi spoje. Nečvor je, dakle, obična struna sa spojenim krajevima. Aleksandrov polinom nečvora je obična konstanta =1. Topološke karakteristike nekog čvora uključuju pojmove kao što je broj preseka (u slučaju nečvora taj broj je =0), vrste preseka - da li nit ide preko ili ispod druge niti na preseku, itd. U svakom slučaju, dakle, postoji tačno utvrdjeno pravilo kojim se nekom čvoru moze pridruziti Aleksandrov polinom, i čvorovi sa istim polinomima su topološki ekvivalentni, tj. mogu se neprekidnim deformacijama transformisati jedan u drugi. I ovo je fundamentalni problem u teoriji čvorova: odrediti koji su čvorovi topoloski ekvivalentni. Staviše, i taj dzemper koji vam je za zimu isplela tetka, baba, je nečvor, jer se prostim povlačenjem niti odmah raspara. Tehnički govoreći, obična kruzna petlja, i vaš omiljen dzmper imaju isti Aleksandrov polinom koji je konstanta =1. Teorija čvorova je dugo bila egzotična matematička disciplina unutar algebarske topologie. Medjutim - a uvek se nadje neko "medjutim" - potpuno nezavisnim putevima fizičari dolaze do zaključka da se elementarne čestice najbolje mogu opisati pomoću strune (zvuči poznato), i teorija čvorova počinje da na velika vrata ulazi u fizičke nauke. Formalnu vezu je teško opisati na ovako malom prostoru, ali mogu samo da nagovstim odakle ona dolazi. Naime, ako posmatramo tri preseka u čvoru, kao na slici dole: 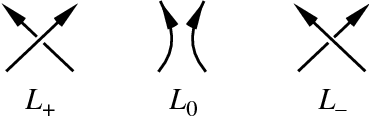 I prvi zovemo pozitivan presek, drugi nulti, a treći negativani, onda prema pravilu o pisanju odgovarajućeg polinoma za taj presek, se lako vidi da P(L+)-P(L-)=x*P(L0), Drugim rečima, da je presek s leva, minus presek s desna = nepresek, tj. da se dva suprotna "zamotaja" poništavaju, što svako dete zna. Ali, ali, ali. Witen je, sa drugim fizičarima, primetio da gornja jednačina mnogo liči na komutacionu relaciju u Kvantnoj mehanici pq-qp=ih, koja, sa svoje strane, na formalan način izrazava Hajzenbergov princip neodredjenosti! Ako nešto "učinimo", i to "odučinimo" u obrnutom redosledu dobijemo broj. Ovo zapazenje je bilo kamen temelja za razvoj savremene teorije struna, ili, Teorije Svega na kojoj najveći fizicari planete i danas rade, pokušavajući da razmrse i razumeju osnovno tkanje kosmosa. [ boxxter @ 10.07.2010. 20:00 ] @
Izvinjavam se svima zbog engleskog, prevescu na srpski izvodjenje dokaza Raselovog paradoksa.
Pominjem marsovce, a niko od moderatora ne prebacuje temu u Ultra MadZone xD. Interesantno.  [ Nedeljko @ 12.07.2010. 07:05 ] @
Citat: boxxter: Kako god, moramo da primetimo, da su ova dva cvora topoloski jednaki u smislu da postoji topoloska transformacija koja ih mapira u jednog u drugi. Takođe su topološki ekvivalentni krugu. Ne postoji topološka razlika između njih. Za njihovo razlikovanje je potrebna malo jača ekvivalencija od topološke. Citat: boxxter: Izvinjavam se svima zbog engleskog, prevescu na srpski izvodjenje dokaza Raselovog paradoksa. Nema potrebe. Ima ga u sredini ove poruke. Citat: boxxter: Pominjem marsovce, a niko od moderatora ne prebacuje temu u Ultra MadZone xD. Interesantno. Ionako je "dokaz" prepisan iz "politikinog zabavnika". [Ovu poruku je menjao Nedeljko dana 12.07.2010. u 08:47 GMT+1] [ Fitopatolog @ 12.07.2010. 07:43 ] @
Citat: Nedeljko: Ionako je "dokaz" prepisan iz "politikinog zabavnika". Što ne mora da znači ništa loše, naprotiv. Samo onaj koji dobro poznaje neku materiju zna da jednostavno priča o njoj. [ Nedeljko @ 12.07.2010. 07:47 ] @
Pa se zato Gedel raspisao na 50-100 strana, jer nije poznavao materiju.
[ Fitopatolog @ 12.07.2010. 07:57 ] @
Mislim da bi (hipotetički) Gedelov tekst za Zabavnik bio itekako interesantan i za one kojima matematika nije dijagnoza. Siguran sam da se u tom tekstu Gedel ne bi junačio sa onima koji slabije poznaju matematiku od njega.
[ Nedeljko @ 12.07.2010. 08:12 ] @
Misliš da se raspisao zbog junačenja? Zbog čega li se onoliko raspisao?
[ Fitopatolog @ 12.07.2010. 08:16 ] @
Gedel je svojim pisanjem pomerio granice ljudskog znanja. Bojim se da ćemo ti i ja (nastavimo li ovako) pomeriti granice ljudske gluposti...
[ Nedeljko @ 12.07.2010. 08:22 ] @
Nemoj meni da pripisuješ svoje zasluge.
[ Fitopatolog @ 12.07.2010. 08:30 ] @
Nikako. Tvoje su više nego dovoljne!
[ Nedeljko @ 12.07.2010. 11:57 ] @
Kakav bezobrazluk! Počeo da iznosi besmislice, pa kad je video da se upleo ko pile u kučinu, meni pripisuje zasluge za to.
[ boxxter @ 12.07.2010. 13:29 ] @
A ne, nemojmo u tom pravcu. Fitopatolog, potpuno si razumeo moju nameru da prezentiram elegantne i pomalo egzoticne dokaze koji inspirisu. I prepoznao si lepotu jednostavnosti, i sposoban si da povuces granicu i napravis razliku izmedju lepote, i banalnog. Moje misljenje je, da je to vrlina.
Citat: Nedeljko: Takođe su topološki ekvivalentni krugu. Ne postoji topološka razlika između njih. Za njihovo razlikovanje je potrebna malo jača ekvivalencija od topološke.] Mislim da nisi u pravu za ovo, i da nisi shvatio sustinu. U svakom slucaju, hvala ti za ucestvovanje na temi, i za link koji si postavio. Voleo bih da ucestvujes i sa nekim elegantnim i egzoticnim dokazom. [ boxxter @ 12.07.2010. 13:46 ] @
Citat: Nedeljko:Takođe su topološki ekvivalentni krugu. Ne postoji topološka razlika između njih. Za njihovo razlikovanje je potrebna malo jača ekvivalencija od topološke. Topološke karakteristike nekog čvora uključuju pojmove kao što je broj preseka (u slučaju nečvora taj broj je =0). [ Nedeljko @ 12.07.2010. 14:24 ] @
Topološka ekvivalencija se zove homeomorfizam i označava postojanje neprekidnog inverzibilnog preslikavanja između dva objekta (topološka prostora) takvog da je i njegov inverz neprekidan. Topološke osobine su osobine koje su zajedničke za ma kakve homeomorfne objekte.
Taj čvor se, baš kao i krug može predstaviti kao slika segmenta [0,1] pri neprekidnom preslikavanju koje je 1-1 uz jedini izuzetak što se 0 i 1 slikaju u istu tačku. Zato su tu potrebne malo jače ekvivalencije od homeomorfizma, jer on čvorove ne razlikuje. Mogao bi da oostaneš i pri homeomorfizmu uz sledeće napomene: 1. Ne posmatraš čvor kao skup tačaka koje mu pripadaju, već kao skup svih tačaka u prostoru koje mu ne pripadaju. 2. Na taj način će i dalje loevi i desni čvor biti ekvivalentni, ali će se čvorovi razlikovati po broju preseka itd. [ Nedeljko @ 12.07.2010. 14:44 ] @
Evo još par linkova o Raselovom paradoksu:
http://www.elitesecurity.org/p354911 http://www.elitesecurity.org/p328289 http://www.elitesecurity.org/p347599 [ boxxter @ 12.07.2010. 15:46 ] @
Fudamenatalni problem u teoriji cvorova je, odrediti koji su cvorovi topoloski ekvivalentni. Takvim razmisljanjem, neces doci do istine.
Na ovim linkovima o Raselovom paradoksu ima toliko toga s cim se ne slazem, tako da izgleda da je matematika koju ja znam, ipak sa marsa. :P Napisacu opet ono, sto sam gore vec naveo, u vezi Raselovog paradoksa. Mozes da das nekom parce papira na kome je napisano- " Recenica napisana na drugoj strani papira, je laz". Kada uzme taj papir, i okrene ga, na drugoj strani pise - " Recenica napisana na drugoj strani papira je istinita". Kod tebe je sve izvesno, i nista te ne zbunjuje, a to me zbunjuje xD. [ boxxter @ 12.07.2010. 15:56 ] @
Mada mi je sve jasno kad procitam sta si ovde napisao. To su za tebe "marginalne zavrzlame".
http://www.elitesecurity.org/t34143-1#328289 Citat: nijedno bitno matematičko tvrđenje ne zavisi od aksiome regularnosti, već samo marginalne zavrzlame kao što je nepostojanje skupa koji bi pripadao samom sebi. [ Nedeljko @ 12.07.2010. 16:17 ] @
Citat: boxxter: Fudamenatalni problem u teoriji cvorova je, odrediti koji su cvorovi topoloski ekvivalentni. Takvim razmisljanjem, neces doci do istine. Ja sam ti naveo definiciju topološke ekvivalentnosti i topoloških svojstava i tu nema šta da se raspravlja, ali dobro, tebi nije jasan pojam definicije. Ekvivalencija čvorova nije topoploško svojstvo. Citat: boxxter: Kod tebe je sve izvesno, i nista te ne zbunjuje, a to me zbunjuje xD. Pa, nauči zasnivanje matematike. No, to nije moguće ako ne znaš pojam definicije i ako se držiš prevaziđenih antičkih teorija. Citat: boxxter: Mada mi je sve jasno kad procitam sta si ovde napisao. To su za tebe "marginalne zavrzlame". Pa, navedi neko bitno matematičko tvrđenje koje zavisi od toga. Da budem još konkretniji, nađi bilo kakvu esencijalnu primenu aksiome regularnosti u bilo kojoj oblasti matematike van osim skupova. Ovo pitanje ima smisla, jer se sve matematičke teorije mogu izložiti unutar TS. [ holononi @ 12.07.2010. 16:38 ] @
{ x | x nije x } je objekat sa zanimljivim svojstvom. To je nešto što jeste ali kad god ga pogledate to nije (za mikročestice je Hajzenbergov princip ograničio preciznost odredjivanja svojstva čestice). Da li postoje takvi matematički objekti (osim iskazi tipa "ono što piše na drugoj strani.." i sličnih) ? Pretpostavimo da treba izračunati tačnu vrednost broja pi. Koliko god cifara izračunate iza vas je konačan broj cifara koje pripadaju broju pi ali je ispred vas beskonačan niz preostalih cifara. I tako uvek imate pi koje nije pi.
[ Nedeljko @ 12.07.2010. 17:00 ] @
Citat: holononi: { x | x nije x } je objekat sa zanimljivim svojstvom. To je nešto što jeste ali kad god ga pogledate to nije To je ništa drugo do prazan skup. [ boxxter @ 12.07.2010. 17:32 ] @
Citat: Nedeljko:Ja sam ti naveo definiciju topološke ekvivalentnosti i topoloških svojstava i tu nema šta da se raspravlja, ali dobro, tebi nije jasan pojam definicije. Ekvivalencija čvorova nije topoploško svojstvo. Ti si naveo definiciju u pogresnom kontekstu, gde se govori o dva cvora koji su kao odraz u ogledalu. Ti sinteticki i napamet ucis definicije, ne ulazeci u sustinu, i totalno promasujuci temu, cak i tamo gde je formalna nauka dala konacni sud. Ta dva cvora su topoloski ekvivalentni, u smislu da postoji topoloska transformacija, koja ih mapira jednog u drugog. Oni su odraz u ogledalu jednog od drugog. Ako ti to nije jasno, mislim da je besmisleno da ti objasnjavam dalje. Citat: Nedeljko:Pa, nauči zasnivanje matematike. No, to nije moguće ako ne znaš pojam definicije i ako se držiš prevaziđenih antičkih teorija. To sto si napisao nije ni blizu definicije topoloske ekvivalentnosti, a ni topologije. Topoloska ekvivalentnost je mnogo kompleksnija. Zato nemoj da pises netacne stvari ovde. A, da. Ti si taj koji je rekao da je definicija stvar nase konvencije. Uvek se zgranem kad vidim da neko ne zna ni osnovne definicije, a samouvereno ucestvuje u nekoj temi. Zbunjujuce je. Kao sto vidis sva matematika je zasnovana na tim, za tebe prevazidjenim antickim teorijama. Temelji formalne nauke su u tim "prevazidjenim antickim teorijama". Ne volim kad je neko zastupnik alternativnog pristupa koji se odrice svakog temelja i znanja. Kao da nista pre njega nije bilo. Ja sam hteo da opisem jednog drugo vidjenje matematickih dokaza, i ukljucio sam istoriju i nastanak samog pojma ili teoreme, da bi bilo interesantnije. I lepse. Raselov paradoks, po njegovom tvrdjenju, nastao je kad je razmisljao o, po tebi, " prevazidjenom antickom Epimenidesovom paradoksu" da su " svi Cretani lazovi". Tebi nije bitan dokaz da je 1+1=2? [Ovu poruku je menjao boxxter dana 12.07.2010. u 18:42 GMT+1] [ boxxter @ 12.07.2010. 18:19 ] @
Tebi izgleda nisu bitni ni dijagonalni argument, i teorija izracunjljivosti. I zakljucci koji proizilaze iz njih.
Pa dobro, bar si uspeo da me nasmejes. =) [ Nedeljko @ 12.07.2010. 18:45 ] @
Ti čvorovi su topološki ekvivalentni baš kao i čvor sa nečvorom, a to što se razmećeš svojim neznanjem me uopšte ne dotiče.
Da, definicija je konvencija da ćemo nešto zvati nekako. To što ti imaš problem sa tim je apsolutno tvoj lični problem u koji nemam nameru da ulazim. Savremena matematika nije zasnovana na tim prevaziđenim teorijama, već na predikatskom računu prvog reda i aksiomatskoj teoriji skupova. Ponavljam, nema ničega što se onda znalo, a što se danas ne zna na mnogo višem nivou. Dijagonalni postupak i teorija izračunljivosti nemaju nikakve veze sa aksiomom regularnosti. [ holononi @ 12.07.2010. 19:08 ] @
Objekat { x | x nije x } u teoriji nije skup jer vodi u kontradikciju pa ne možemo reći da li je prazan ili ne. Medjutim u realnosti se ovakvi problemi rešavaju "sečenjem Gordijevog čvora".
Naime ako imate dva lažova koji jedan drugog optužuju ne možete se pouzdati u njihove iskaze. Ali uvek možete pronaći neki drugi način da utvrdite istinu. [ Nedeljko @ 12.07.2010. 19:20 ] @
[ Fitopatolog @ 12.07.2010. 20:52 ] @
Citat: Nedeljko: Kakav bezobrazluk! Počeo da iznosi besmislice, pa kad je video da se upleo ko pile u kučinu, meni pripisuje zasluge za to. Dobro-de Nedeljko, ne žesti se. Ipak smo svi mi sa ovog foruma na neki način prijatelji... [ Nedeljko @ 12.07.2010. 20:55 ] @
Ovo je već mnogo bolje.
[ holononi @ 12.07.2010. 21:09 ] @
Upravo sam na taj objekat mislio inače bih napisao "različit", osim toga naglasio sam "objekat". Hvala što si se potrudio da ispišeš formule.
[ Fitopatolog @ 12.07.2010. 21:16 ] @
Citat: Nedeljko: Ovo je već mnogo bolje. Mora biti tako kada prijateljujemo još od teme http://www.elitesecurity.org/t41172-2 [ boxxter @ 12.07.2010. 23:46 ] @
Citat: boxxter:Ta dva cvora su topoloski ekvivalentni, u smislu da postoji topoloska transformacija, koja ih mapira jednog u drugog. Oni su odraz u ogledalu jednog od drugog. Citat: Nedeljko: Ti čvorovi su topološki ekvivalentni baš kao i čvor sa nečvorom. Da, definicija je konvencija da ćemo nešto zvati nekako.i. Citat: Nedeljko: nijedno bitno matematičko tvrđenje ne zavisi od aksiome regularnosti, već samo marginalne zavrzlame kao što je nepostojanje skupa koji bi pripadao samom sebi. Citat: Nedeljko: Savremena matematika nije zasnovana na tim prevaziđenim teorijama, već na predikatskom računu prvog reda i aksiomatskoj teoriji skupova. Ponavljam, nema ničega što se onda znalo, a što se danas ne zna na mnogo višem nivou. Dijagonalni postupak i teorija izračunljivosti nemaju nikakve veze sa aksiomom regularnosti. =) [ boxxter @ 12.07.2010. 23:53 ] @
Citat: boxxter: "Matematika moze da se definise kao predmet u kome mi nikad ne znamo o cemu govorimo, niti da li je tacno to sto govorimo." Bertrand Russell. 1872�1970 Citat: Nedeljko: Rasel je poznat po raznim glupostima, kao na primer da matematička knjiga ne može biti i korektna i čitljiva, koje samo pokazuju koliki je bio nnjegov stepen nerazumevanja matematike. =))) [ boxxter @ 13.07.2010. 13:28 ] @
Dijagonalni argument
Neka R bude skup, a F funkcija koja govori da je x ∈ R , podksupa R, F(x) ⊂ R. Drugim recima, 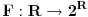 . .Takva funkcija moze da se predstavi vizuelno u kvadratu R × R. Za svako x ∈ R, F(x), moze da se opise u vertikalnom segmentu. Zvacemo ih G(x), G(x) = {x} × F(x). Sada, za neko x, G(x), sece dijagonalu D = {(x, x)}, G(x) ∩ D ≠ Ø; i za neko x, G(x), ne sece dijagonalu G(x) ∩ D = Ø. Naravno G(x) ∩ D ≠ Ø je ekvivalentno x ∈ F(x), i G(x) ∩ D = Ø je ekvivalentno x ∉ F(x). Pogledajmo sad skup Z, za svako x Z = {x ∈ R: G(x) ∩ D = Ø} = {x ∈ R: x ∉ F(x)}. Teorema: Za nijedno x ∈ R, F(x) = Z Dokaz: Pretpostavimo, da nasuprot toga, neko a, F(a) = Z. Mozemo onda da postavimo pitanje, da li je, ili nije a ∈ Z. Videcemo da obe mogucnosti vode u kontradikciju. Pretpostavimo prvo da je a ∈ Z. To bi znacilo da G(a) ∩ D = Ø, implicira da a ∉ F(a), a to znaci da a ∉ Z. Pretpostavimo sad da a ∉ Z. To bi znacilo da G(a) ∩ ≠ Ø, implicira da a ∈ F(a), a to znaci da a ∈ Z. [ boxxter @ 13.07.2010. 13:37 ] @
Jasno je da su neizracunjljivost realnih brojeva, i Raselov paradoks, u sustini, istog porekla.
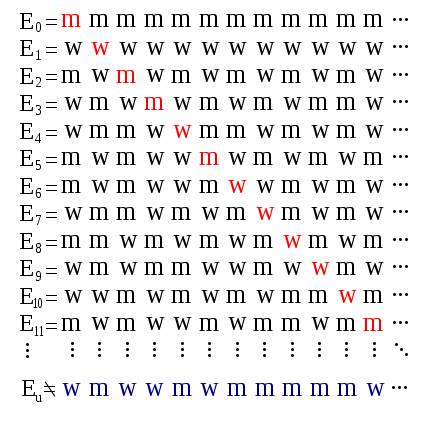 [ boxxter @ 13.07.2010. 13:49 ] @
Georg Ferdinand Ludwig Philipp Cantor, tvorac teorije skupova,(i dijagonalnog argumenta), koja je postala fudamentalna teorija u matematici. Cantorova teorija implicira beskonacnost, beskonacnosti. Cantorov rad je od velokog filozofskog znacaja, i on je bio svestan toga.
Poincaré je govorio da su Cantorove ideje smrtne bolesti, i obicna infekcija za matematicku disciplinu. Govorili su jos za njega da je naucni sarlatan, i da upropascava omladinu. [ Nedeljko @ 13.07.2010. 14:07 ] @
Citat: boxxter: Jasno je da su neizracunjljivost realnih brojeva, i Raselov paradoks, u sustini, istog porekla.[/img] Neizračunljivost realnih brojeva? Da nisi slučajno mislio na nešto drugo? Poreklo Raselovog paradoksa je u Kantorovoj teoremi o patritivnom skupu. No, to i dalje nema veze sa aksiomom regularnosti. [ boxxter @ 13.07.2010. 17:10 ] @
Teorema sa ociglednim dokazom.
Teorema: Ovo je jedina teorema u ovom mom postu. Dokaz: Dokaz je ocigledan. [ boxxter @ 13.07.2010. 17:19 ] @
Citat: Nedeljko: Neizračunljivost realnih brojeva? Da nisi slučajno mislio na nešto drugo? Ko zna. Mozda jesam, a mozda i nisam. I ko zna gde su koreni svega, i sta sve ima zajednicku sustinu i poreklo. [ Nedeljko @ 13.07.2010. 17:21 ] @
Šta znači "neizračunljivost realnih brojeva"?
[ holononi @ 13.07.2010. 18:28 ] @
Možda nije najzanimljiviji dokaz ali je svakako inspirativan
Paradoks lopte (http://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox) Otkrili su ga Banach i Tarski a govori da se jedna lopta (unutrašnjost i površina) može rastaviti na konačan broj (mora bar 5) delova i nakon (samo) translacije i rotacije ovih delova dobijaju se dve lopte svaka sa osobinom da je kongruentna sa polaznom loptom. Za sada nema praktičnu primenu pa je razlog više da ga radoznali prostudiraju. [ boxxter @ 13.07.2010. 19:27 ] @
The diagonal argument was not Cantor's first proof of the uncountability of the real numbers;
it was actually published much later than his first proof, which appeared in 1874. However, it demonstrates a powerful and general technique that has since been used in a wide range of proofs, also known as diagonal arguments by analogy with the argument used in this proof. The most famous examples are perhaps Russell's paradox, the first of Gödel's incompleteness theorems, and Turing's answer to the Entscheidungsproblem. http://en.wikipedia.org/wiki/Cantor%27s_diagonal_argument Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument. Cantor's first uncountability proof was published in 1874, in an article that also contains a proof that the set of real algebraic numbers is countable, and a proof of the existence of transcendental numbers.[1] http://en.wikipedia.org/wiki/C...27s_first_uncountability_proof [ boxxter @ 13.07.2010. 19:37 ] @
Reductio ad absurdum.
[ holononi @ 14.07.2010. 04:06 ] @
Ako se pozivate na Wikipedia nema potrebe da pastirate sadržaj originala osim ako ne dajete vaš prevod (što je nepotrebno). Dovoljno je da referencirate link ali je nužno da iznesete vaš stav i razloge zašto se na to pozivate. Ovako razmislite, možde ste postovali neupotrebljiv teks.
Sve što ima na Wikipedia mnogi na ovom forumu su manje-više davno pročitala (na bilo koji način) bar kad je reč o matematici. Šta više, za neke se može reći "rasli su zajedno". [ boxxter @ 14.07.2010. 09:09 ] @
Dobro. Vi u stvari poznajete celu wikipediu. Mislim da treba citirati odredjeni navod iz wikipedie, i kopirati ga ovde, da bi se izdvojio odredjeni deo teksta.
Ako si pratio razgovor, govorio sam o tome da su neizracunjljivost skupa realnih brojeva, i Raselov paradoks, sustinski iste vrste. Ali neko se ne slaze sa tim. Ne znam da li si pratio razgovor. Postoji negde vec izveden dokaz, a na to nas navode posledice koje proizlaze iz dijagonalnog argumenta. Ali i to vec verovatno znate. Tako da nije potrebno da izvodim dokaz ovde. [ Nedeljko @ 14.07.2010. 09:33 ] @
Ponavljam. Šta je formulacija "neizračunljivosti skupa realnih brojeva"?
[ boxxter @ 14.07.2010. 10:54 ] @
"Uncountable" redirects here. For the linguistic concept, see Uncountable noun.
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the natural numbers. http://en.wikipedia.org/wiki/Uncountable_set The best known example of an uncountable set is the set R of all real numbers; Cantor's diagonal argument shows that this set is uncountable. The diagonalization proof technique can also be used to show that several other sets are uncountable, such as the set of all infinite sequences of natural numbers (and even the set of all infinite sequences consisting only of zeros and ones) and the set of all subsets of the set of natural numbers. http://en.wikipedia.org/wiki/Uncountable_set#Examples [ Sini82 @ 14.07.2010. 11:02 ] @
Nemoj učiti matematiku sa wikipedie. Nisi dobro preveo tekst, vjerovatno ga nisi dobro ni shvatio. Ne radi se o neizračunjivosti nego o neprebrojivosti skupa realnih brojeva. Nije Kantorov dijagonalni argument, nego Kantorov dijagonalni postupak.
[ holononi @ 14.07.2010. 11:07 ] @
@boxxter
Nemoj karikirati, nisam napisao "Vi u stvari poznajete celu wikipediu.", baš naprotiv, dobro sam birao reči. Ako pod "neizračunljivosti skupa realnih brojeva" podrazumeš neprebrojivost intervala realnih brojeva tada se može reći da postoji sličnost izmedju konstrukcija 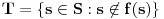 i skupa u Raselovom paradokusu. Možete pogledati na primer http://wapedia.mobi/en/Cantor%27s_diagonal_argument. i skupa u Raselovom paradokusu. Možete pogledati na primer http://wapedia.mobi/en/Cantor%27s_diagonal_argument.Neka objekte klasifikujemo po tipovima. S jedne strane postoje strogo jednaki tipovi a s druge postoje tipovi koji su univerzalni u tom smislu da termovi toga tipa imenuju sve tipove do na izomorfizam. U verzija Raselovog paradoksa svaki tip poseduje zatvoren term i svi termovi istog tipa su jednaki. [ Nedeljko @ 14.07.2010. 11:23 ] @
Citat: boxxter: "Uncountable" redirects here. For the linguistic concept, see Uncountable noun. In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the natural numbers. http://en.wikipedia.org/wiki/Uncountable_set The best known example of an uncountable set is the set R of all real numbers; Cantor's diagonal argument shows that this set is uncountable. The diagonalization proof technique can also be used to show that several other sets are uncountable, such as the set of all infinite sequences of natural numbers (and even the set of all infinite sequences consisting only of zeros and ones) and the set of all subsets of the set of natural numbers. http://en.wikipedia.org/wiki/Uncountable_set#Examples Da, to nije neizračunljivost, već neprebrojivost. Da, tu se koristi dijagonalni argument, mada može i drugačije. Pretpostavimo da je  niz svih realnih brojeva. Konstruišimo nizove niz svih realnih brojeva. Konstruišimo nizove 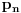 i i 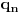 na sledeći način: na sledeći način: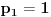 , , 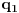 je najmanji prirodan broj veći od je najmanji prirodan broj veći od  takav da je takav da je 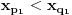 . .Za 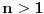 je je 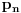 najmanji prirodan broj veći od najmanji prirodan broj veći od 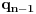 takav da je takav da je 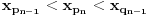 i i 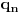 najmanji prirodan broj veći od najmanji prirodan broj veći od 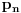 takav da je takav da je 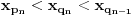 Lako se dokazuje da je definicija korektna, da je 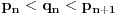 i da za i da za 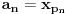 i i 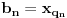 važi važi 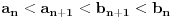 . .Za 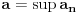 i i 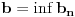 je je 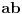 , pa postoji , pa postoji 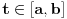 . Neka je . Neka je  najmanji prirodan broj takav da je najmanji prirodan broj takav da je 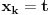 . Jasno je da je . Jasno je da je 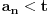 , tj. da , tj. da 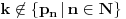 i slično za i slično za 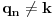 . Razmotrimo prvi član u nizu . Razmotrimo prvi član u nizu 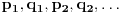 koji je veći od koji je veći od  . Ako je to . Ako je to 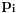 , onda je to u suprotnosti sa njegovim izborom, a ako je to , onda je to u suprotnosti sa njegovim izborom, a ako je to 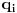 , opet je to u suprotnosti sa njegovim izborom. , opet je to u suprotnosti sa njegovim izborom.Kraj. [ miki069 @ 15.07.2010. 03:06 ] @
Verzija Raselovog paradoksa:
"Pretpostavimo da postoji selo sa samo jednim berberinom. Takođe, pretpostavimo da su svi muškarci u selu obrijani: neki se briju sami, a neke brije berberin. Zvuči razumno da se berberin ponaša na sledeći način: on brije sve one, i samo one ljude koji se ne briju sami. Po ovom scenariju, postavlja se sledeće pitanje: Da li berberin brije samog sebe? Kada se postavi ovo pitanje, uočava se da je situacija predstavljena ovim uslovima u stvari nemoguća: Ako berberin ne brije sebe, mora da poštuje svoje pravilo, i da brije sebe. Ako berberin brije sebe, po svom pravilu neće brijati sebe." Šta je ovde paradoks? Brije ga žena. Inače izbor "dokaza" do sada je ravan nuli, jer nisu lepi a traže se najlepši. Predlažem da napustite filozofiju i da se vratimo na matematiku. Dakle: Te-1 "Centralni ugao, nad istim kružnim lukom, je duplo veći od periferijskog". Posledice. Te-2 "Kosinusna teorema za trougao", specijalan slučaj - Pitagorina teorema Te-3 "Sinusna teorema za trougao" Te-4 "Heronov obrazac" Te-5 "Kroneker-Kapelijeva teorma" Te-6 "Kramerova teorema" Te-7 "Teorema o dijagonalizaciji matrice (preko nula karakterističnog polinoma)" Te-8 "Bezuov stav", poledice Te-9 "Osnovni stav algebre" Te-10 "Hornerova šema" Te-11 "Faktorizacija polinoma" Te-12 "Vešestruke nule polinoma" Te-13 "Vijetove formule" Te-14 "Osobine racionalnih nula polinoma" Te-15 "Moavrove formule" . . . [Ovu poruku je menjao miki069 dana 15.07.2010. u 04:16 GMT+1] [ Nedeljko @ 15.07.2010. 07:07 ] @
Ala su ti to lepi dokazi... Ma, daj. To jesu standardne teoreme, ali ništa više od toga.
[ Nedeljko @ 15.07.2010. 07:16 ] @
[ Fitopatolog @ 15.07.2010. 07:25 ] @
Jako je lep, samo ko voli...
[ miki069 @ 15.07.2010. 10:43 ] @
Možda nisu lepi ali su iz matematike.
Ne iz filozofije. Oću da vas vratim na matematiku. [ Nedeljko @ 15.07.2010. 11:16 ] @
OK, znači, Gedelove teoreme nepotpunosti, Raselov paradoks, čvorovi, topološka ekvivalentnost i aksiomatska teorija skupovanisu iz matematike, nego iz filozofije.
[ zzzz @ 15.07.2010. 11:27 ] @
[ Nedeljko @ 15.07.2010. 13:25 ] @
[ miki069 @ 15.07.2010. 13:51 ] @
Paskalov trougao:
1 1 1 2 1 1 3 3 1 1 4 6 4 1 ............... kojim se formiraju binomni koeficijenti je takođe nešta zbog čega se zavoli matematika. [ Nedeljko @ 15.07.2010. 14:15 ] @
Gde je tu dokaz? Ovde treba postavljati dokaze.
[ miki069 @ 15.07.2010. 14:33 ] @
Dokaz ide ako se narod izjasni da je tvrđenje dobro.
Tvrđenje glasi: "k-ti element n-tog reda Paskalovog trougla je binomni koeficijent (n povrh (k-1))." Dokaz: za prvi red (n=1) je tačno jer je (1 povrh 0) = (1 povrh 1) = 1. za bilo koji sledeći red (n>1) razlikujemo 2 slučaja: a) za krajnji levi (k=1) i krajnji desni element (k=n+1) je tačno jer je (n povrh 0) = (n povrh n) =1 b) za bilo koji između (1<k<n+1) trebe pokazati da je (n povrh k) = ((n-1) povrh (k-1)) + ((n-1) povrh k). Slika tog ključnog dela dokaza je u prilogu. Legenda: Povrh (hrvatski) = Iznad (srpski).  [Ovu poruku je menjao miki069 dana 15.07.2010. u 15:44 GMT+1] [ boxxter @ 15.07.2010. 15:42 ] @
Citat: Citat: Nedeljko: OK, znači, Gedelove teoreme nepotpunosti, Raselov paradoks, čvorovi, topološka ekvivalentnost i aksiomatska teorija skupovanisu iz matematike, nego iz filozofije. U pravu je Nedeljko. Poceli smo od teorija koje su imale krucijalan i sustinski uticaj na matematiku, i njeno shvatanje. Neverovatnu stvar si izgovorio, da to nije matematika. Tvoj stav pomalo govori o danasnjem shvatanju matematike. Verovatno nisi jedini koji tako misli. [ Nedeljko @ 15.07.2010. 15:49 ] @
Nedeljkova teorema: Velika većina matematičara smatra da je najteža i najvažnija ona oblast kojom se oni bave.
Dokaz: Eksperimentalno provereno. [ Fitopatolog @ 16.07.2010. 19:06 ] @
Uopšte nismo dobro počeli. Kao matematičari, prvo smo trebali definisati koji dokazi spadaju u tzv. LEPE, a zatim treba da definišemo i neku metriku u skupu lepih rešenja. Bez ovoga nećemo daleko stići...
[ Nedeljko @ 16.07.2010. 22:44 ] @
Kad smo već kod dokaza i teorije skupova, da priložim i jedan pogrešan "dokaz" da je aksioma izbora posledica ostalih aksioma teorije skupova. Zadatak je naravno bio da se nađe greška u dokazu. Ovo je, da se pohvalim, moja umotvorina.
http://www.elitesecurity.org/p1930349 [ holononi @ 22.07.2010. 04:39 ] @
Citat: Kako se teoreme može dokazati eksperimentalno ? [ mjanjic @ 30.08.2010. 00:30 ] @
Jedan od najlepsih dokaza je vezan za Ojlerovu konstantu 'c' (EulerGamma u Wolfram Matematici).
Dakle, treba dokazati da je red 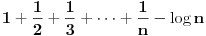 opadajuci i ogranicen odozdo i da je ta granicna vrednost veca od nule. opadajuci i ogranicen odozdo i da je ta granicna vrednost veca od nule.U dokazu se nekoliko puta koriste nejednakosti bez kojih bi dokaz bio gotovo nemoguc: 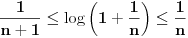 Takodje, jos jedan od veoma lepih dokaza je Euklidov dokaz da prostih brojeva ima beskonacno: http://primes.utm.edu/notes/proofs/infinite/euclids.html [ Nedeljko @ 30.08.2010. 21:25 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|