Evo ja cu pokusati
vjerovatno je ovo jednacina



a ovo uslov koji zadovoljavaju rjesenja i


Ako datu jednacinu malo transformisemo, dobit cemo:





opsti oblik kvadratne jednacine je
pa je prema tome





ako sada napisemo viettovu formulu



onda prema datom uslovu imamo da je



posto je




to je



valjda je to TO :)

da ne bih mijenjao ovo rjesenje, koje ti moze posluziti, malo sam bolje pogledao postavku zadatka, i vjerovatno si pogrijesio prilikom pisanja uslova, koji kod tebe glasi
1:X1+1X2=1
vjerovatno si mislio na
1:X1+1:X2=1 gdje si izostavio jednu dvotacku (ko fol znak dijeljenja) pa bi uslov bio



Slicno je kao u prethodnom zadatku, samo se koriste obije viettove formule.




opsti oblik kvadratne jednacine je
pa je prema tome





Sada dati uslov malo transformisemo:

**

ako sada napisemo viettovE formulE




i iskoristimo ih u jednacini ** onda ona postaje

***

posto je




to je ***






odakle slijedi da je
ili

Posto mi je dosadno, i nemam sta raditi, provjerit cemo ova rjesenja koja sam ja dobio.
Za p=1 data jednacina postaje
cija su rjesenja
i

kad to uvrstimo u uslov

dobijemo
sto jeste tacno

za p=3 jednacina postaje

cija su rjesenja

i

kad to uvrstimo u uslov

dobijemo


vidi se da je i za p=3 uslov zadovoljen.
Pozz



_{[Ovu poruku je menjao Kolins Balaban dana 11.03.2007. u 12:32 GMT+1]}

Hajde mi molim te ako budes znao resi i ovo:
Za koje vrijednosti koeficijenta C funkcija f(X)=1:2*x*x-4x+c, ima minimum jednak -8
-za nadjeno C nacrtaj graf ove funkcije
-za koje X(R) je tada f(X) rastuca funkcija?

Ako znas pomagaj molim te imam kontrolni a nemam pojma ovo





Ogi

Znaci imamo kvadratnu funkciju



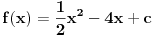
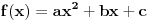
Kao sto vec znamo opsti oblik kvadratne funkcije je gdje extrem (minimum ili maximum) zavisi od predznaka vodeceg clana a uz . Ako je a<0 tada funkcija ima maximum, a ako je a>0 tada funkcija ima minimum. posto je u datoj funkciji a>0, to ona ima minimum.
x kordinata tacke extrema (cesto ces cuti i termin TJEMENA funkcije, kad je u pitanju kvadratna funkcija) kvadratne funkcije je



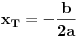
a y koordinata extrema kvadratne funkcije je

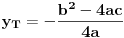
ili

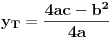
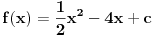
iz funkcije imas da je




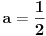
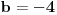
a posto treba da ima minimum jednak -8, to je
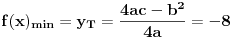
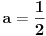
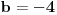
uvrstavajuci , i u prethodnu jednacinu, dobijemo



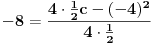
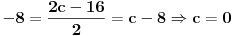
Prema tome funkcija ima oblik



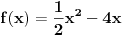
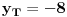
za graf kvadratne funkcije potrebne su ti nule te funkcije i koordinate tjemena. u zadatku ti je vec data jedna koordinata tjemena, odnosno , pa je potrebno naci x koordinatu tjemena po formuli
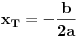
odnosno

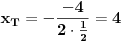
prema tome TJEME te funkcije (u nasem slucaju je to minimum) je tacka
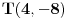
Treba naci jos nule te funkcije, a to cemu uraditi na sljedeci nacin:


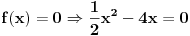
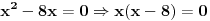
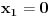
odakle se dobije da je i
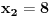
sada mozemo nacrtati grafik te funkcije

[att_img]

sada treba odrediti interval, u kome je data funkcije rastuca. to se vidi direktno sa slike
kad x raste od 4 do 8, y raste od -8 do 0, zatim kad x raste od 8 do + beskonacno, y raste od 0 do + beskonacno. Eto to je TO :) pozz i sretno na kontrolnom.
mali dodatak: to zadnje sto sam napisao rijecima, mozes napisati drugacije:

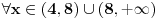
i na tom inervalu data funkcija RASTE!

_{[Ovu poruku je menjao Kolins Balaban dana 11.03.2007. u 16:04 GMT+1]}

Pozdrav prvo bih htio da ti se zahvalim na rjesenim zadacima (vidi se da ces biti inzinjer) zelio bih da te pitam gdje si isao u srednju jer ja idem u Mostaru,i matematiku mi predaje Hamid Poturovic ako te zanima.
Pa hvala ti jos jednom a ako budem imao jos problema mogu li ti se obratiti za pomoc????


Ogi

hehehe pa fino pise lokacija: Srednja bosna, a Mostar nije u srednjoj bosni :P naravno da se mozes obratiti ako ti bude trebala pomoc ;)

E opet ja imam sada jedan problem koji glasi ovako:
Rijesi nejednacinu X*X-2X+3
---------- >0
3+2X-X*X




Pozdrav

Ovakve zadatke radiš na sledeći način: kada je vrednost razlomka veća od nule, kao u ovom slučaju, tada i brojilac i imenilac moraju biti istog znaka. Postavljaš dva slučaja. Prvi slučaj je da su i brojilac i imenilac veći od nule, a drugi je da su i brojilac i imenilac manji od nule.

U prvom slučaju, dakle, rešiš obe kvadratne jednačine tako da obe budu veće od nule i nađeš presek ta dva skupa rešenja.

U drugom slučaju rešiš obe kvadratne jednačine tako da obe budu manje od nule i nađeš presek ta dva skupa rešenja.

Na kraju nađeš uniju rešenja za prvi i za drugi slučaj i to je rešenje zadatka.

Eto, koristeći ova pravila, uradićeš zadatak bez problema, a ako ipak nešto bude zapelo, ti javi.

OK, pomognem ti jos ovaj puta, ali iduci puta necu ne budes li mi napisao dokle si ti SAM dosao, i gdje si tacno zapeo. Ovako ti ne pomazem bas mnogo.

ako dobro vidim, u pitanju je nejednacina



najprije rastavis i brojnik i nazivnik na faktore. to bi izgledalo ovako:

brojnik: koliko se moze vidjeti, brojnik nema realnih nula (izracunas vrijednist diskriminante, i vidis da je ona manja od nule). a to znaci da grafik ne sijece x osu ni u jednoj tacki, a to opet znaci da je za ili za . odgovor na to pitanje ce nam dati predznak vodeceg clana (clana uz ). Posto je taj clan jednak 1, tz. da data funkcija ima minimum, odnosno da je citava pozitivna (pogledaj prethodne moje postove u ovoj temi), pa prema tome vrijedi
za

nazivnik:


pa sad imas sljedecu situaciju



posto nam je vec za , onda mora biti (razlomak je veci od nule, samo ako su brojnik i nazivnik istih predznaka, oba pozitivna ili oba negativna, a posto je brojnik pozitivan za , to mora biti i nazivnik pozitivan). nadjimo sad interval na kojem je nazivnik pozitivan:


posto je u pitanju proizvod, on je pozitivan ako su oba faktora istih predznaka, odnosno imamo neka dva slucaja:
1. SLUCAJ:
i
i odnosno

2.SLUCAJ
i
i ovdje je rjesenje prazan skup (ne postoji broj veci od 3, a manji od -1)

prema tome rjesenje nejednacine je i to je rjesenje i polazne nejednacine . Eto toliko od mene, valjda nisam nigdje pogrijesio :D

izvini sto ti nisam govorio gdje sam stao evo od sada cu imam zadatak koji glasi:
Napisi kvadratnu jednacinu cije je jedno rijesenje


X1= 7/2+i korjen iz 3

E sad ja sam to racionalisao ali ne znam kako dalje jer nista vise nije dato,a ima dosta zadataka koji su takvog izgleda a u knjizi nema objasnjenja

Vodi računa da ako su rešenja kvadratne jednačine kompleksni brojevi, tada su ta rešenja konjugovano-kompleksna (znači, realni delovi jednaki, a imaginarni su suprotnog znaka). Ako ovo imaš u vidu, sasvim ćeš lako odrediti kako glasi kvadratna jednačina:

, gde su i kompleksna rešenja (konjugovano-kompleksna), a je proizvoljna konstanta.