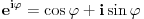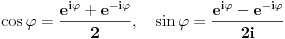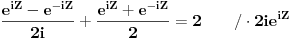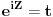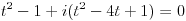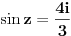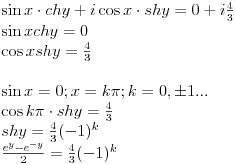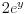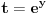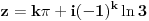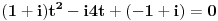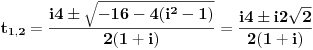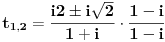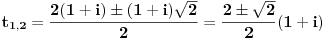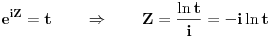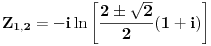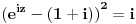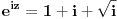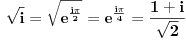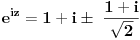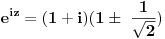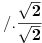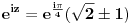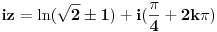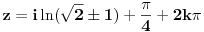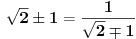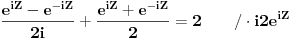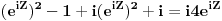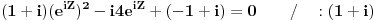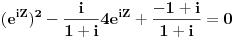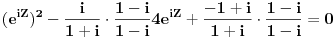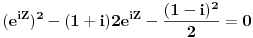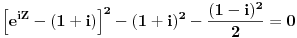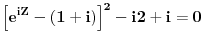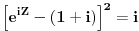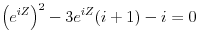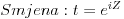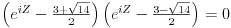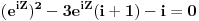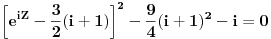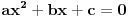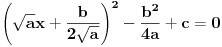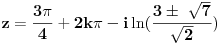[ spaka-s @ 18.03.2007. 13:17 ] @
| Komplexna analiza i komplexni brojevi. Naci sva rjesenja jednacine: 1.) sinZ + cosZ=2 2.) sinZ - cosZ=3 Bilo kakav savjet kako se radi ovaj tip zadataka. Pokusavao sam ali mi ne ide, a nemam literature... Hvala unaprijed. |