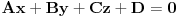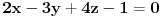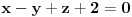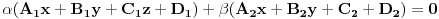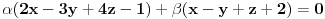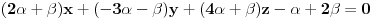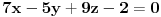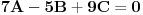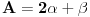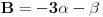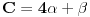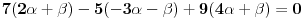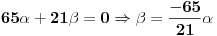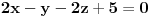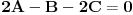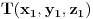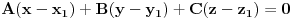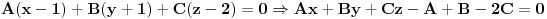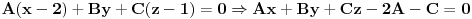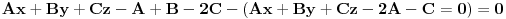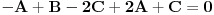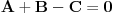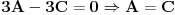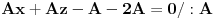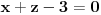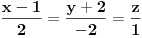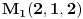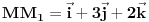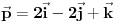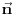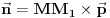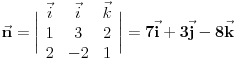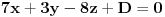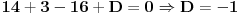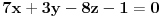Evo ja cu pokusati da pomognem, iako sam dosta ovih stvari zaboravio, pa mi nemoj zamjeriti ako pogrijesim :)
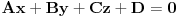
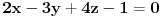
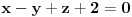
ZADATAK1. ovdje se kaze da neka ravan prolazi kroz presjek ravni i . Presjek dvije ravni predstavlja PRAVAC, a skup ravni koje se sijeku po tom pravcu (presjeku dvije ravni) zovemo PRAMEN ravni. Ti si spomenuo SNOP ravni. Tri ravni se sijeku u jednoj tack, a skup ravni koje prolaze kroz tu jednu tacku (presjeka tri ravni) se zove SNOP ravni. Prema tome ovdje treba koristiti jednacinu pramena ravni koaj glasi:

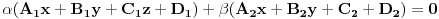
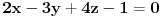
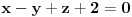
Pramen ravni koji zadrzi presjek ravni i ima sljedecu jednacinu

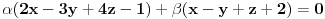
odnosno *
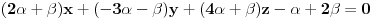
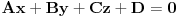
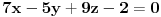
Posto trazena ravan treba biti normalna na ravan onda su im normalni i NORMALNI vektori tih ravni, odnosno mozemo iskoristiti uslov normalnosti koji ce u tom slucaju glasiti
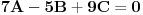
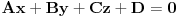
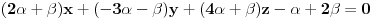
Posto trazena ravan pripada pramenu ravni onda mozemo napisati da je:



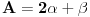
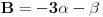
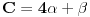
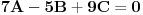
Kad te jednacine uvrstimo u uslov dobijemo sljedecu jednacinu:



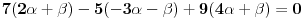
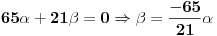
Kad to vratimo u jednacinu * i podijelimo je sa dobijemo trazenu ravan.
Moram sada ici, a pomogao bih ti i oko ostalih zadataka. Nadam se, da u ovom nisam pogrijesio. Pozz

Evo da probam rijesiti i preostale zadatke.
ZADATAK2:
Neka je trazena ravan data jednacinom . posto je po uslovu zadatka ta ravan normalna na , to mozemo napisati uslov normalnosti njihovih NORMALNIH vektora, tj.
*
Jednacina ravni kroz tacku je pa kad tu uvrstimo zadate tacke A i B dobit cemo
A(1,-1,2): **
B(2,0,1): ***

Oduzimanjem jednacine *** od jednacine ** dobijemo da je



****

Sada cemo posmatrati sistem jednacina * i **** Sabiranjem tih jednacina dobijemo:
*****
Ako jednacinu ***** zamjenimo npr u jednacini * dobit cemo da je B=0
Prema tome imamo da je
A=C i B=0
Kad to vratimo u neku od jednacina ** ili *** dobit cemo (ja cu vratiti u jednacinu **) trazenu ravan:

ZADATAK3:
p:
tacka
Neka je M(1,-2,0) neka tacka na pravoj p

Sa slike se vidi da je
iz jednacine prave imamo da je
Neka je vektor normalan na ravan, sa slike se vidi da je

odnosno



Prema tome, trazena ravan ima oblik . Posto ta ravan sadrzi tacku , to ce nam pomoci da nadjemo D, odnosno

Trazena ravan je


[att_img]

Hvala jarane, svaka cast.