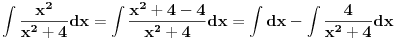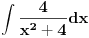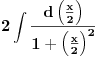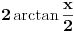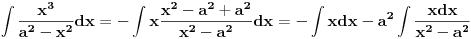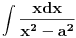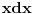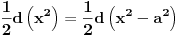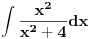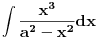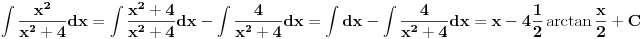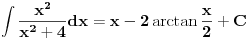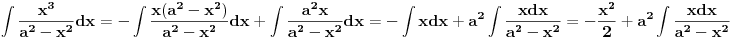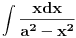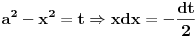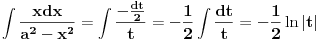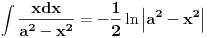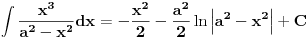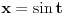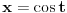[ jhondoe @ 22.03.2007. 19:15 ] @
|
| Imam problem sa integralima.
kako se rješavaju ovi integerali:
x2/(x2+4)dx i
x3/(a2-x2)dx
to su zadaci iz demidoviča (1068 i 1069) i ta dva tipa zadataka ne znam rješiti
pa ako ima koja dobra duša da mi pokaže postupak rješavanja.
btw: ima li negdje postupci na koji su rješeni zadaci iz demidoviča |
[ Daniel011 @ 22.03.2007. 19:46 ] @
Prvi integral radiš na sledeći način:
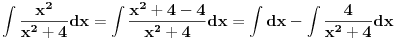
Integral
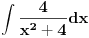
posle sređivanja možeš napisati kao
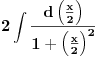
, što je tablični integral i iznosi
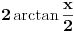
.
Sa drugim integralom uradiš sledeće:
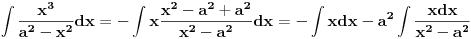
U integralu
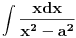
brojilac
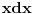
napišeš kao
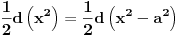
i time taj integral svedeš na tablični.
[ Kolins Balaban @ 22.03.2007. 19:59 ] @
Hajd da ja pokusam. Koliko vidim rijec je o integralima
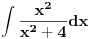
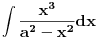
Rjesenje prvog bi ovako nekako izgledalo:
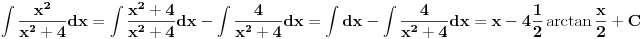
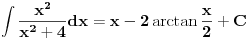
Rjesenje drugog bi ovako nekako izgledalo:
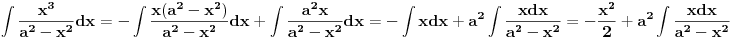
Treba naci integral
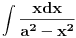
uvedemo smjenu
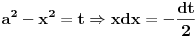
sada je
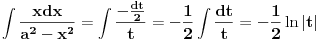
nakon vracanja smjene dobijemo da je
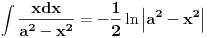
Prema tome rjesenje pocetnog integrala je
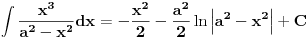
Eto, valjda je to TO. Nadam se, da sam pomogao. Pozz
[ Kolins Balaban @ 22.03.2007. 20:00 ] @
Hehehe izgleda da smo u isto vrijeme rjesavali zadatke.
[ Daniel011 @ 22.03.2007. 20:08 ] @
Eh Kolinse, kako ti uvek ubiješ ljudima želju da savladaju zadatke, time što im uvek pružiš na tacni ceo urađen zadatak.

Ovaj forum nije zamišljen da ljudi nauče da budu prepisivači, nego da im se objasni postupak ako negde zapne, ali da se i sami malo pomuče da dođu do rešenja. Slažeš se?
[ Kolins Balaban @ 22.03.2007. 20:15 ] @
Hmmmm, pa mozda si u pravu, a mozda i nisi. Ako neko ima zelju da na nauci, onda ce pogledati dio rjesenja, zatvoriti oci, i nastaviti raditi sam. Ovaj decko, ako sam dobro skontao, prvi puta radi int ovog tipa, pa sam i radi toga uradio ovo detaljno, da pokusa sam skontati fazon na koji se radi ovaj tip int. Sve ovo radim iz najbolje namjere, a ne zato sto je meni zanimljivo tipkati tex. ipak je to zamorno, slazes se? Dosta brze bi islo napisati to na papir, pa skenirati, ali nemam skener :D :)
[ jhondoe @ 27.03.2007. 07:34 ] @
Hvala momci. Rješaval sam integrale i prije, ali sad se nisam mogo sjetit takvih "trikova". Rješil sam neke zadatke iz Demidoviča pa sad rješavam parcijalno pa ćemo se vjerojatno opet čuti.
[ Sa_nji_ca @ 01.10.2008. 21:13 ] @
I meni treba vasa pomoc, kako se resava sledeci integral>
∫x^2/√(1-x^2 )dx
unapred hvala!!
[ Daniel011 @ 01.10.2008. 21:25 ] @
Smenom
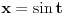
(ili
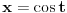
).
[ miki069 @ 01.10.2008. 22:54 ] @
Ili u brojiocu oduzmes 1 i dodas 1 pa podelis na 2 integrala od kojih je drugi arcsin(x) a prvi polutablican - moze se resiti parcijalnom intergracijom.
Ali manja muka ti je smenom koju ti je dao Danijel011. Ostane ti posle te smene x = sin(t)...integral od (sint)^2 koji resavas ili parcijalnom integracijom ili direktno primenom:
(sint)^2 = (1-cos(2t))/2 posle cega imas 2 elementarna integrala.
Resenje je: I = 1/2*(t) - 1/4*sin(2t) + C
Ajde sad ti sama vrati resenje da bude zavisno od x a ne od t.
[ Sa_nji_ca @ 02.10.2008. 17:00 ] @
Hvala puno!!!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.