Hajde da ja pokusam, ako sam dobro shvatio zadatak. Treba dokazati, da dati razlomak, za bilo koji n iz prirodnih brojeva, nece biti prirodan broj (ili bolje receno, CIO pozitivan broj). U pitanju je razlomak



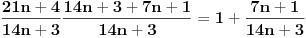sada treba pokazati, da razlomak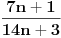



nikad nece biti cio (pozitivan) broj. To je i ocito, jer je brojnik uvijek veci od nazivnika za bilo koje
n iz prirodnih brojeva, pa prema tome taj razlomak ne moze biti prirodan broj. valjda je to to.

Neka je i . Oduzimanjem oe dve jednacine dobijas da .
Kako je , tj. , pa se razlomak ne moze skratiti.

Kakve ovo ima veze sa (ne)mogucnoscu skracivanja razlomka??

Ja sam shvatio, da treba dokazati da ne postoji ni jedan prirodni broj n, za koji je , gdje je k prirodan broj, npr. da imamo ovu situaciju (lupam)