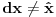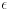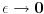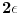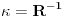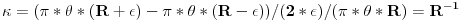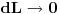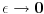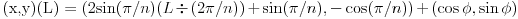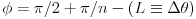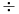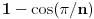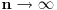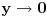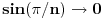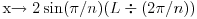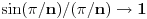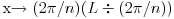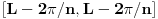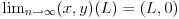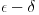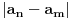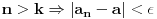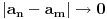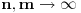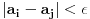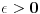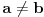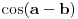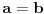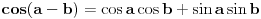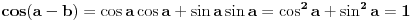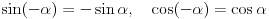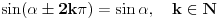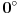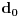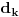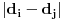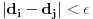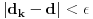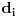|
|
[ galet@world @ 30.03.2007. 08:39 ] @
|
|
Kako se u principu definišu različitosti među krivim linijama međusobno, ili kako se definiše različitost između krive i prave linije suštinski.
Ako presečemo list papira na dva dela pravom linijom, onda će dužina preseka na jednom delu papira biti jednaka dužini preseka na
drugom delu papira.
Ako, međutim, iz papira isečemo krug - da li je obim kruga jednak obimu rupe u papiru?
Ako jeste onda kružnica nije kriva linija, a ako nije za koliko se ti obimi razlikuju i kako te razlike zavise od oblika i veličine krivih?
|
[ petarm @ 30.03.2007. 09:28 ] @
Prava je za mene kriva linija kojoj poluprecnik krivine tezi beskonacno.
[ zoran_dojkic @ 30.03.2007. 11:07 ] @
Tačka, u matematici, nema veličinu, linija i površina nemaju debljinu. To su matematički aksiomi.
Sečenje papira je neka druga nauka. U mašinstvu postoji pojam Tolerancija mere. Krug isečen iz lista papira ima manji prečnik od prečnika rupe koja je ostala u listu. Dimenzije se označavaju milimetrima, tako da bi i prečnik isečenog kruga i prečnik rupe na crtežu bio označen istom merom (cifrom), ali bi u toleranciji (odstupanju od mere) bilo naznačeno da je krug "mera minus određeni deo mm", a rupa "mera plus određeni deo mm). Ovo je uprošćeno objašnjenje za one koji nisu upućeni u Tolerancije mere.
Kriva linija čiji poluprečnik krivine teži beskonačnom je kriva linija.
[Ovu poruku je menjao zoran_dojkic dana 01.04.2007. u 13:18 GMT+1]
[ Kolins Balaban @ 30.03.2007. 13:09 ] @
hmmmm "Kriva linija čiji poluprečnik krivine teži beskonačnom je kriva linija." mozda si mislio na pravu liniju?
[ mcetina2 @ 30.03.2007. 20:17 ] @
Fantasticno pitanje galet!
Ukratko -- sta ti je prava linija ako ti je prostor kriv? :)
Definicija koja prvo pada na pamet je:
Prava linija je najkrace rastojanje izmedju dve tacke.
tj.
Linija koja spaja dve tacke je prava ako je medju svim linijama koje spajaju te dve tacke najkraca.
Nazalost, istpostavlja se da ova definicija ima neke neprijatne osobine. Zamisli npr. dve tacke na sferi i najkracu liniju izmedju njih. Ako drugu tacku pomeras sve dalje i dalje od prve, u nekom trenutku dve tacke naci ce se dijametralno suprotno jedna drugoj. U tom trenutku postojace beskonacno puno "najkracih" linija izmedju dve tacke. Drugim recima po gorenavedenoj definiciji prava linija izmedju dve dijametralno suprotne tacke nije definisana.
Zato ovu definiciju modifikujemo kao:
Linija koja spaja dve tacke A i B je prava ako je u odnosu na sve male deformacije u odnosu na nju samu, ekstremna -- ili najkraca ili najduza ili iste duzine.
Ova definicija je zgodna jer omogucava da prave linije sracunamo na samo na osnovu izraza za duzinu proizvoljne infinitezimalne linije u prostoru (metrike prostora).
Meni je zanimljivo da Euklidovi postulati u stvari definisu nezakrivljen prostor (Riemann tensor === 0; postoji koordinatni sistem (x,y,z) koordinatni sistem takav da su prave linije u njemu l = (x0,y0,z0) + t(dx,dy,dz) i duzine pravih linija sqrt(Dx^2 + Dy^2 + Dz^2) ), iako uopste ne pricaju o geometriji preko koordinata.
[ galet@world @ 30.03.2007. 20:24 ] @
Ili vi niste shvatili pitanje ili ga ja nisam jasno postavio. Probaću drukčije:
Da li je konveksna strana krive duža od konkavne?
Ako nije duža zašto je onda ta linija kriva (iskrivljena)?
Ako je ta strana duža - kolika je i kakva je ta razlika u dužini između tih strana?
Ako je odgovor da kriva nema dve strane nego samo jednu - od čega potiče iskrivljenost krivih?
Ako neko nije matematičar, onda je bolje da ne odgovara, jer mi ne znamo pa zato pitamo matematičare koji možda znaju.
[ mcetina2 @ 30.03.2007. 20:36 ] @
Sto se poluprecnika krivine tice, ovaj pojam iziskuje uzimanje izvoda vektora tangentnog na krivu duz te krive. Bolje receno, iziskuje poredjenje tangentnog vektora krive sa samim sobom duz same krive.
U zakrivljenom prostoru ovo pitanje poredjenja vektora u razlicitim tackama prostora *veoma* je netrivijalno i zove se parallel-transport vektora. Ispostavlja se da odabir parallel-transport mehanizma u stvari potpuno odredjuje geometriju zadatog prostora.
Takodje vazi da ako od svih mogucih poredjenja vektora odaberemo takvo poredjenje da za bilo koja dva originalna vektora u i v u bilo kojoj tacki A na krivi i za dva odgovarajuca prenesena vektora u' i v' u tacki B na toj istoj krivi vazi (u,v) = (u',v') gde je (u,v) skalarni proizvod vektora, onda ova definicija prave linije preko krivine krive i moja definicija preko ekstremizacije duzine krive postaju ekvivalentne.
Zanimljivo je medjutim da uslov (u,v) = (u',v'), cesto nazvan metric-compatibility of parallel-transport, nije dovoljan da se jednoznacno odredi parallel transport proizvoljnog vektora po proizvoljnoj krivi! Dodatni parametar se zove torzija (torsion tensor) i odredjuje parallel-transport vektora po krivi koja je normalna na taj vektor (za razliku od parallel-transporta tangentnog vektora duz samog sebe u slucaju ispitivanja da li je neka kriva prava).
Cinjenica da radi merenja precnika krivine krive na klasican nacin moramo da uvedemo parallel-transport koji eto u nasem slucaju *ispada* da je dobro definisan (bez obzira na torziju) meni puno ide na nerve. Prosto neelegantno! Zato mnooogo vise volim definiciju koju sam naveo u prethodnoj poruci.
P.S.
Za OTR je naravno potreban parallel-transport vektora. Metric-compatiblity ima fizickog smisla. Naime, ako si u liftu koji slobodno pada, uglovi i rastojanja izmedju predmeta koji sa tobom slobodno padaju nece se menjati. Torzija se medjutim dosta proizvoljno deklarise da je 0. I dalje nisam naisao na neko dobro fizicko objasnjenje zasto. Znam doduse da je John Baez ovoj temi posvetio nekoliko clanaka (koje mozda nisam dovoljno pazljivo procitao).
[ mcetina2 @ 30.03.2007. 20:50 ] @
Jos jedan komentar, pogotovo za petarm:
Ako je kriva u 3D, lako je pricati o torziji i bi-torziji. Izvodjenje Kartanovih jednacina krive medjutim implicitno koristi parallel-transport vektora u (ravnom) 3D prostoru u kome se kriva nalazi.
Nazalost, kao i u mnogim drugim primenama vektorskog diferencijalnog racuna, nacin na koji se 3D parallel-transport koristi u izvodjenju Kartanovih jednacina je dosta mutan. Ovo je glavni razlog zasto *mrzim* 3D vektorski racun. Cim uzmes nekartezijske koordinate ili se pak prebacis u kriv prostor, the whole fucking thing breaks. A onda se na jedvite jade trudis da nadjes razloge zasto.
Zato olaksajmo zivot i sebi i drugima:
No action at a distance.
No parallel-transport without a curve.
No cross-products.
No implicit identification of vectors and 1-forms (i.e. 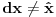 )
Ako ne mozes da odradis neki proracun pod ovim uslovima, mozes unapred da znas da proracun nece proci u krivolinijskim koordinatama ili pak u krivom prostoru. Primer1: magnetno polje strujne konture (Biot-Savart zakon). Ako proracun prodje pod ovim uslovima, videces odmah razlike izmedju pravog i krivog prostora. Takodje, moci ces lako da koristis sfericnu ili cilindricnu ili... simetriju problema.
[ mcetina2 @ 31.03.2007. 02:38 ] @
Pogledao sam malo pazljivije raniju diskusiju pa mi je nesto zapalo za oko.
Galetova ideja o poredjenju duzina levih odnosno desnih delova krive odgovara u stvari mojoj definiciji.
Jer, zamisli da kriva ima neku malu "debljinu". Ovu "debelu" krivu mozemo da posmatramo kao jednu pravu (infinitezimalno tanku) krivu koja odgovara centroidu debele krive + tanke krive koje opisuju obim debele krive. Ako je nasa debele kriva dovoljno tanka, ove krive po obodu bice infinitezimalno udaljene od centralne referentne krive.
Sada:
Ako je kriva koja odgovara centroidu po mojoj definiciji prava, onda njene male (infinitezimalne) promene nece uticati na njenu duzinu. To znaci da ce duzina svih tankih krivih po obodu debele krive biti jednaka medjusobno i jednaka duzini krive u centru.
Vazi i obrnuto -- ako sve krive po obodu imaju istu duzinu kao i kriva u centru, onda se duzina krive u centru nece promeniti ako istu infinitezimalno deformisemo. Stoga je kriva u centru po mojoj definiciji prava.
Zato: sve strane "infinitezimalno zadebljane" krive su jednake duzine <=> kriva je prava. Ovo vazi u *bilo kojem* prostoru.
[ galet@world @ 31.03.2007. 08:33 ] @
Zamisli, Marko, neki kružni venac ili deo kružnog venca proizvoljne širine.
Možeš li reći kolika je dužina tog kružnog venca ili nekog njegovog dela?
[ mcetina2 @ 31.03.2007. 18:17 ] @
Mogu -- uzmem tanak konac po kome sam ravnomerno (poredeci sa samim sobom) naneo referentne oznake. Onda polosim konac duz pravca ciju duzinu hocu da merim. Posto je konac tanak, njegovo savijanje ne utice na to koliko dobro funkcionise za merenje duzine.
Ako na ovaj nacin izmerim unutrasnji obim venca i spoljasnji obim venca, zakljucicu da su razliciti. Stoga zakljucujem da je oblik venca zakrivljen.
Jos jednom, ovde je jako bitno da moj lenjir tj. konac bude tanak u odnosu na krivinu onoga sto merim. Ovo "tanak" se moze rigorozno matematicki definisati.
[Ovu poruku je menjao mcetina2 dana 31.03.2007. u 19:52 GMT+1]
[ galet@world @ 31.03.2007. 20:19 ] @
Citat: mcetina2: Ako na ovaj nacin izmerim unutrasnji obim venca i spoljasnji obim venca, zakljucicu da su razliciti. Stoga zakljucujem da je oblik venca zakrivljen.
Bez obzira na širinu venca uvek će unutrašnji obim venca biti manji od spoljašnjeg, pa je venac zakrivljen i onda sledi:
venac je zakrivljen zato što mu je unutrašnji obim manji od spoljašnjeg.
To važi uvek - čak i ako je venac predstavljen jednom linijom - zato što je ta linija (infinitezimalni venac) zakrivljena.
Venac nije izgubio svojstvo zakrivljenosti zbog toga što mu je širina 0 cm.
Venac je i pri toj širini zadržao svojstvo zakrivljenosti zato što mu je konkavna strana drukčija od konveksne.
Kad bi te strane bile jednake onda to ne bi bio venac ( odnosno kriva) nego prava.
Odavde sledi važan (moj) zaključak da se kriva linija ne može dobiti "krivljenjem" prave linije i obrnuto.
To su različite pojave i svako poređenje je neprincipijelno.
Prava linija se ne može iskriviti niti kriva ispraviti.
[ mcetina2 @ 31.03.2007. 21:19 ] @
A i, joojj galet --
intuicija o mnogim stvarima ti je dobra ali, kao sto si sam rekao, nisi matematicki potkovan. To dovodi do mnogih konfuzija.
U matematici linija -- bilo prava, bilo kriva -- nema debljinu. Tacka. Zato ne mozes matematicki *tek tako* da pricas direktno o razlicitoj duzini unutrasnje i spoljasnje strane linije. Tacka.
Medjutim, tvoju intuiciju mozemo da spasemo putem sledeceg granicnog procesa:
Zamisli da imas beskonacno tanku (matematicku) liniju:
-----------------------
Onda iz svake tacke te linije mozes normalno da povuces jednu drugu linijcu.
|*|*|
|*|*|
----------
|*|*|
|*|*|
Onda po toj linijci sa obe strane originalne linije mozes da udaris recke jednako i jako malo (razdaljina 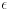 ) udaljene od centra prvobitne linije:
x*x*x
|*|*|
----------
|*|*|
x*x*x
Ove dve serije recki -- isto tako beskonacno tanke -- prave dve dodatne linije "parallelne" i na rastojanju 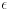 od prvobitne -- beskonacno tanke -- linije. Zajedno sa prvobitnom linijom, ove dve linije grade "traku" konacne debljine. Ova "traka" pak veoma lici na ono o cemu, koliko se meni cini, ti razmisljas.
Ako dve strane ove trake tj. dve reckaste linije imaju razlicitu duzinu, prvobitna linija je kriva. Ako imaju istu duzinu, prvobitna linija je prava.
Ukratko --
Matematicki je netacno da pricas o dve strane matematicke linije i o njihovim razlicitim duzinama (jer linija nema "dve strane")!
Medjutim, tvoja intuicija moze da se izvuce putem granicnog procesa kada pustis 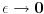 .
Dalje, po ovom kriterijumu pravu liniju moguce je kontinualno deformisati tako da postane kriva. Naravno, i pri najmanjoj konacnoj deformaciji ona ce postati kriva. Zato tebi izgleda da su "prava" i "kriva" linija dva sasvim drugacija pojma (ili nesto jeste 0 ili nije 0).
Medjutim, umesto da govorimo o kategoricnim pojmovima "pravo" i krivo, moguce je uvesti meru zakrivljenosti linije kao granicna vrednost
(duzina spoljasnje krive - duzina unutrasnje krive)/ 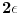 /(duzina centralne krive)
kada duzina centralne krive -> 0 i 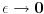 .
Ovo svodi na Cartanovu 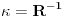 zakrivljenost krive gde je R tzv. "poluprecnik krivine". U slucaju kruga u ravnom prostoru, R odgovara poluprecniku tog kruga. Zbilja:
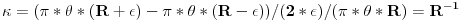
P.S.
Pazljiva analiza granicnih vrednost 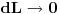 i 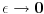 od izuzetne je vaznosti za logicku konsistentnost izlaganja.
Nazalost, granicni procesi poput ovog koji sam naveo mogu da budu veoma suptilni -- matematicarima je trebalo >150 godina (od Njutna do Weierstrass-a, Cantor-a i drugih) da ovakve procese koji se cesto koriste u fizici logicki potkuju. Zato pazljivo!
[ zoran_dojkic @ 01.04.2007. 12:14 ] @
Citat: mcetina2: U matematici linija -- bilo prava, bilo kriva -- nema debljinu. Tacka. Zato ne mozes matematicki *tek tako* da pricas direktno o razlicitoj duzini unutrasnje i spoljasnje strane linije. Tacka.
Da si pročitao šta sam ja rekao na početku, ne bi ni pisao sve prethodno.
Citat: Tačka, u matematici, nema veličinu, linija i površina nemaju debljinu. Prazna rasprava, kao mnogo puta na ovom forumu (molim one koji nemaju smisla za direktan odgovor da se uzdrže od pisanja). [ galet@world @ 01.04.2007. 13:18 ] @
Evo pokušao sam da "ispravim krivu Drinu" pa ne ide
Vidi prilog!
[ mcetina2 @ 02.04.2007. 00:35 ] @
galet -- u stvari, ide.
Sve linije koje si opisao jesu krive. Konkretno, svim svojim tackama osim tacaka preloma imaju krivinu jednaku krivini pocetnog kruga. Medjutim, prelaz na granicnu vrednost je suptilan i nisi ga korektno odradio. Konkretno, granicna vrednost tvog niza linija *jeste* prava linija.
Intuitivan razlog za to je da ako svi elementi odredjenog konvergentnog niza pripadaju odredjenom skupu, njihova granicna vrednost ne mora da pripada istom tom skupu. Tako su svi elementi reda 1/n gde su n prirodni brojevi pozitivni (krivi). Medjutim, granicna vrednost reda (0) niti pripada redu niti je pozitivna (kriva).
Ovo je moguce dokazati ako uvedemo x-y koordinatni sistem i parametrisemo u tom koordinatnom sistemu tvoju izlomljenu liniju u zavisnosti od rastojanja L po liniji.
Ako je poluprecnik prvobitnog kruga 1 i ako ga izdelimo na n delova:
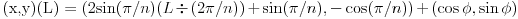
gde je
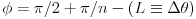
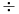 oznacava ceo rezultat a  ostatak pri deljenju.
Maksimalna vrednost |y| u ovom slucaju iznosi 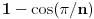 . Kada 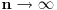 , ocigledno da za sve L 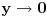 ravnomerno.
Ostaje da razmotrimo x. Medjutim, ako 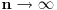 , 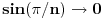 . Stoga
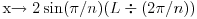
Medjutim, ako 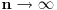 , 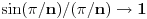 pa
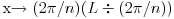
medjutim, ovaj izraz ce uvek da se nalazi u 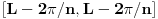 . Kako n tezi beskonacnosti, ovaj interval tezi tacki L.
Stoga
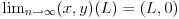
A (x,y) = (L,0) za L od nula do 2pi je pak prava linija.
Dakle -- ukratko --
Sve linije koje si ti nacrtao *jesu* krive. Medjutim, njihova granicna vrednost je prava!
[Ovu poruku je menjao mcetina2 dana 02.04.2007. u 01:51 GMT+1][ mcetina2 @ 02.04.2007. 00:44 ] @
zoran_dojkic, zamolio bih te da pazljivo procitas i pokuses da razumes konstrukciju za razlikovanje prave i krive 1D linije koju sam naveo u poruci koju sam citiras (ono:
|*|*|
|*|*|
----------
|*|*|
|*|*|
)
Upravo u toj poruci, umesto da diskusiju svodim na metafizicku/filozofsku raspravu o tome da li idealna linija ima debljinu (za koju bi se vecina ljudi slozila da je banalna) pokazujem kako je galetovu intuiciju o debelim linijama moguce formalizovati. Na taj nacin ovaj nacin razmisljanja postaje korisan u okviru matematike u kojoj su sve linije beskonacno tanke. Stavise, ova intuicija je itekako korisna i vodi do pojmova tipa Riemann-ove krivine.
[ galet@world @ 02.04.2007. 15:42 ] @
Sad je na mene red da kažem da „ne ide“
Marko:
Citat: Medjutim, prelaz na granicnu vrednost je suptilan i nisi ga korektno odradio. Konkretno, granicna vrednost tvog niza linija *jeste* prava linija.
Prelaz na graničnu vrednost nisam „odradio“ nikako – ni korektno ni nekorektno. Pre svega takav
prelaz nije dozvoljen. „Suptilnost“ takvog prelaza je sasvim nekorektna. Evo zašto:
Svaki deo kružnice – i veći i manji imaju istu zakrivljenost – ona se ne menja nego je konstantna
i nezavisna od veličine tih delova tj. ta zakrivljenost ne teži nuli. Otkud odjedanput skokovit „suptilan“
prelaz na nultu zakrivljenost kad takve težnje nema?
Skokovit prelaz znači napuštanje određene pojave i njenih svojstava i prelaz na drugu, drukčiju
pojavu koja ima drukčija svojstva – odjednom bez postepenog prelaza iniciranog nekom težnjom.
Ali šta time dokazujemo izuzev različitosti među tim pojavama?
[ mcetina2 @ 02.04.2007. 20:29 ] @
galet, ne razumem sasvim kuda ciljas osim metafizike/filozofije.
Mozda ce ovo da pojasni stvari.
Od vremena Newton-a pa do kraja 19. veka matematicari su se mucili da upravo ovaj pojam "teznje" nekog niza nekoj granicnoj vrednosti dobro logicki potkuju. Newton i Laplace su o ovakvim "teznjama" puno pricali i stavise koristili ih za izvodjenje (tacnih) fizickih rezultata. Medjutim, niko nije imao matematicki cvrstu podlogu za ove pojmove.
Krajnji veliki rezultat ovog rada Weierstrass-a i ostalih u 19. veku je uvodjenje pojmova metrickog prostora, topologije i 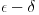 definicija granicne vrednosti. 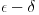 procedura omogucava da se u matematici poveze jedna vrsta objekta (granicni niz) sa drugom (granicna vrednost) koja *zaista* moze da ima veoma drugacije osobine od prve (granicnog niza).
Nacin na koji se ovaj pojam uvodi u mnogo cemu prati nasu intuiciju o pojmu limita. Konkretno, uvede se izvesan pojam rastojanja izmedju pojedinacnih elemenata  niza. Onda se primeti da kada n i m postanu veliki, rastojanje 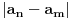 postane veoma malo. Intuitivno, kada n->beskonacnost, svi elementi niza se nekako trpaju na gomilu.
Zatim se uvodi granicna vrednost kao tacka nagomilavanja svih elemenata niza. Drugim recima, ona tacka u cijoj bilo kojoj okolini se nalazi beskonacno puno elemenata niza.
Matematicki precizno, granicna vrednost a niza  je takva da za svaki pozitivan realan broj 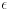 postoji prirodan broj k tako da 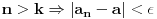 (Weirstrass). U mnogim slucajevima moguce je logicki dokazati da je ova tacka jedinstvena.
Ovo nagomilavanje je po meni intuitivno neophodno oko bilo koje granicne tacke. Zato, opet mo meni, bilo koji intuitivan pojam granicne tacke niza mora da se poklopi sa ovim matematickim.
Bitno:
Posto smo ovako matematicki definisali jedinstvenu granicnu vrednost konvergentnog niza ( 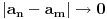 kada 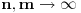 ), moguce je sa svakim konvergentnim nizom (pojmom prve vrste) dovesti u vezu granicnu vrednost (pojam druge vrste).
Onda reci da ne mozes da poredis niz i granicnu vrednost jer su to babe i zabe malo je bez veze. Jer -- sama granicna procedura (izlozena gore) daje nacin da se ova dva pojma dovedu u vezu, analizaraju i porede.
P.S.
Nezavisno sta mislis o pravim/krivim linijama i nezavisno od tvog stava prema ovoj diskusiji, preporucio bih ti da sednes i pokusas da shvatis 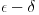 definiciju granicne vrednosti u matematici. Ova definicija je na logicki stabilne temelje postavila sav danasnji diferencijalni racun (integrale, izvode, etc.) i matematicku analizu. Takodje se radi o jednom od najvecih matematickih podviga 19. veka.
Topao pozdrav,
Marko [ mcetina2 @ 02.04.2007. 21:01 ] @
galet -- izvini --
ja sam se opet zaneo u mojoj prici a nisam razmislio o tvom problemu i ukazao na sustinski problem. Kriv sam malo ko' djokic :)
Sa stanovista epsilon-delta definicije, tvoj problem sastoji se u tome sto uobicajeno rastojanje izmedju krivih koje se koristi za nalazenje granicne vrednosti tvog niza krivih -- naime --
"|kriva1 - kriva2| = maksimalno rastojanje izmedju tacaka A i B na krivama 1 i 2 takvim da je rastojanje po krivi 1 od pocetka krive 1 do tacke A jednako rastojanju po krivi 2 od pocetka krive 2 do tacke B"
*nije povezano* sa krivinom kriva 1 i 2.
Zato je granicni proces koji sam naveo u pretprosloj poruci, inace sasvim matematicki korektan, u stanju da sve krivine ispegla.
*******************************************************************
Ovde medjutim nailazimo na jedan problem. Ako zelimo matematicki precizno da pricamo o granicnoj vrednosti, moramo nekako da uvedemo pojam "rastojanja" izmedju dve krive. Ne izmedju pojedinacnih tacaka vec izmedju dve citave krive kao dva objekta.
Definicija koju sam naveo (max. rastojanje izmedju odgovarajucih tacaka dve krive) je po meni dosta intuitivno jasna....ono takodje dovodi do jedinstvene granicne krive kao sto sam vec spomenuo.
Ako ti se moja granicna vrednost ne svidja, ja bih onda trazio drugu definiciju rastojanja izmedju dve krive. Konkretno, neki pojam rastojanja izmedju dve krive koji bi se osvrtao na zakrivljenost odgovarajucih krivih.
Tu sam ti medjutim malo skeptican.... u stvari, malo vise... pokusaj da se u rastojanje dve krive uvede neka vrsta izvoda kao sto je zakrivljenost moze da dovede do mnogih patologija....
*************************************************
Kratak summary:
epsilon-delta granicni proces koji sam opisao u prethodnoj poruci dovesce do glatkog prelaska sa niza na granicnu vrednost sa stanovista mere rastojanja izmedju tacaka u prostoru |a_n - a_m| koju koristis za nalazenje granicne vrednosti. Druge karakteristike datih elemenata niza, iako glatke od jednog do drugog elementa, mogu se skokovito promeniti pri (inace dobro matematicki definisanom preko |a_n-a_m| rastojanja) prelasku na granicnu vrednost.
[ galet@world @ 03.04.2007. 09:25 ] @
Citat: Zato je granicni proces koji sam naveo u pretprosloj poruci, inace sasvim matematicki korektan, u stanju da sve krivine ispegla.
Koliko graničnih vrednosti ima to peglanje?
Na taj način možeš neku krivu prepeglati u bilo koju drugu krivu i reći da joj je to granična vrednost. Zašto
bi kriva sa nultom zakrivljenošću imala prednost nad ostalim krivim, izuzev zbog naše želje da to učinimo.
Kako granična vrednost može zavisiti od naše želje?
Kad smo već kod peglanja onda i to peglanje, konkretno, znači postepeno, a ne skokovito smanjenje
zakrivljenosti, a granična vrednost bi bila zakrivljenost podloge.
Granični proces koji navodiš nema ničeg zajedničkog sa peglanjem shvaćenim principijelno.
Kriva linija se ne može ispeglati isto tako kao što ne možemo ispeglati sfernu površinu
[ mcetina2 @ 03.04.2007. 20:26 ] @
> Koliko granicnih vrednosti ima to peglanje?
Sa kriterijumom rastojanja izmedju dve krive koji sam naveo u prethodnoj poruci i sa redom krivih koje si ti specificirao, postoji jedinstvena granicna vrednost.
> Na taj nacin mozes neku krivu prepeglati u bilo koju drugu krivu i reci da joj je to granicna vrednost.
Kao sto sam rekao, granicna vrednost zavisi od niza krivih (koji si ti specificirao) i mere rastojanja (koju sam ja ponudio (*)). Ako hoces, mozes da *pokusas* da uzmes drugi kriterijum mere. Medjutim, ja tvrdim da ce ti biti veoma tesko da takav kriterijum nadjes, da on da rezultat drugaciji od mog, a da u isto vreme ima osobine koje bi ocekivao od neke intuitivne mere razlike izmedju dve krive.
Konkretno, ako ocekujes da niz koji si definisao ima granicnu vrednost, moras da se pobrines da po tvojoj meri, za svako 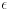 postoji prirodan broj n tako da za sve i,j>n, 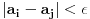 . Inace tvoj niz krivih nece biti konvergentan i nece imati granicnu vrednost.
> Zasto bi kriva sa nultom zakrivljenoscu imala prednost...
Moj kriterijum razdaljine ne obraca paznju na zakrivljenost. Koliko se meni cini, samo ispada tako (it turns out) da ima prednost.
> Kako granicna vrednost moze zavisiti od nase zelje?
Pa moze -- u matematici je bilo koja postavka (po nasoj zelji) OK pod uslovom da nije kontradiktorna i da je korektno logicki izvedena.
Napredak matematike sastoji se u tome da nas nasa intuicija dovode do novih postavki/aksioma ili novih pretpostavki (teorema) o kojima onda razmisljamo ne bi li bolje razumeli siri matematicki sustav/konstrukt o kome pricamo. U ovom smislu ja i citam i odgovaram na tvoje poruke. Trudim se da razumem tvoju intuiciju. Onda se trudim da je formalizijuem i proverim da li je logicki konzistentna.
*****************************************************
I jedna generalna primedba na dijalog do sada:
Imas veoma dobru intuiciju koja navodi na veoma zanimljive diskusije. Medjutim, po meni, ne citas dovoljno pazljivo ono sto drugi pisu i ne nadovezujes se na to. Imam utisak da pitas jednu stvar, ja se onda potrudim da to formalizujem i izdiskutujem sa stanovista matematike i fizike koju znam a usput i sam shvatim i naucim nesto novo. Medjutim, onda umesto da se nadovezes na logicki sled onoga sto sam izneo i na taj nacin vise doprineses diskusiji, ti iz tvoje intuicije postavis gomilu novih pitanja.
Ostavljas mi dosta nezahvalan posao odgovaranja uvek u trci za tvojim pitanjima, prakticno bez bilo kakvog intelektualnog "hvala".
(*)
rastojanje izmedju krivih = max. razdaljina izmedju tacke A na krivi 1 i tacke B na krivi 2 takve da je rastojanje tacke A od pocetka krive 1, mereno duz krive 1 jednako rastojanju tacke B od pocetka krive 2, mereno duz krive 2.
Primeti, jos jednom:
1) Ovaj kriterijum bliskosti krivi ne obraca paznju na njihovu zakrivljenost.
2) Po ovom kriterijumu bliskosti [ galet@world @ 04.04.2007. 21:10 ] @
Citat: Ostavljas mi dosta nezahvalan posao odgovaranja uvek u trci za tvojim pitanjima, prakticno bez bilo kakvog intelektualnog "hvala".
Dobro – da malo zamenimo uloge.
Moj stav u principu je sledeći:
1. Ako delimo bilo kako definisanu liniju, površinu ili prostor na beskonačno mnogo delova onda
a) tu pojavu time ne uništavamo.
b) svaki beskonačno mali deo zadržava osnovna svojstva („genetski materijal“) pojave od koje je nastao.
c) upravo zbog toga i samo zbog toga moguć je obrnut (reverzibilan) proces sastavljanja pojave od tih delova.
2. Protivim se savremenom tretmanu nule ovako
a) postoji nula koja nema dimenziju i ona označava nepostojanje.
b) postoji nula koja ima dimenziju i određena svojstva.
c) bijektivno preslikavanje se pogrešno tumači.
Ima toga još, ali da te ne zamaram previše. Pitaj!
Vrlo rado ću da zahvalim ako mi pokažeš da sam u zabludi - zasad mi se čini da bi moglo biti i obrnuto, ali i da jeste
tako ja ne bih tražio zahvalnost.
P.S.
Mislim da bi tvoji odgovori bili jasniji i očigledniji ako bi se malo potrudio da ih ilustruješ. [ mcetina2 @ 06.04.2007. 05:56 ] @
U standardnoj analizi koja potice od ranije navedenog Weirstrass-a, koja se predaje po fakultetima i koju sam ja ucio, nikada se ne definisu "beskonacno male" ili "beskonacno velike" velicine. Umesto toga, svi granicni procesi formulisu se preko epsilon-delta iskaza poput onoga koga sam naveo u prethodnoj poruci. Ovi iskazi pak barataju sa iskljucivo konacnim velicinama ("za svaki pozitivan broj epsilon postoji n tako da za sve k>n...."). Zato u okviru ove analize prosto ne mogu nesto da "rastavim na beskonacno mnogo delova" ili posmatram "beskonacno male delove" necega. Upravo u ovom izbegavanju "beskonacno malih" velicina sastoji se znacaj Weirstrass-ovog rada. I upravo ova Weirstrassova prica o beskonacno malim velicinama bez beskonacno malih velicina je nesto zbog cega brucosi sirom sveta ceskaju glavu.... :))
Naravno, galet ne bi bio galet da nije nabo' nesto zanimljivo. Naime, u danasnjoj matematici postoje verzije analize (grana matematike koja se bavi kontinualnim pojavama) u kojima se eksplicitno definisu beskonacno male velicine. Ovo se vodi pod nazivom nestandardna analiza i potice iz XX veka (Weirstrass je radio pocetkom XIX-og). Medjutim, ova analiza se retko (citaj: nikada) koristi medju naucnicima/fizicarima. I za matematicare je izgleda manje zanimljiva (manje se koristi) od standardne analize.
Sve u svemu, ja nestandardnu analizu ne znam i nemam vremena da ucim :(( (iako mi zvuci mnogo zanimljivo) Zato zaista ne mogu da ponudim nikakv komentar u glavnom pravcu galetovog posta. Pogotovo mi je zao mi je jer znam da u nestandardnoj analizi postoje pojmovi tipa pozitivne nule, negativne nule, beskonacno malog pozitivnog broja, zbira beskonacno puno beskonacno malih delova koji je konacan, etc.
Takodje moram da kazem da nemam vremena da u saradnji sa galetom pokusam da izgradim nestandardnu analizu u koju bi uvrstio pozitivnu nulu, beskonacno male velicine, etc. Jer, ako su se matematicali mucili sve do pocetka XX veka.... kako cemo onda galet i ja igde stici? :)
Zato najbolje sto mogu je da uradim je da drzim predavanja po ovom forumu iz analize po Weierstrass-u.....
tacka  zove se granicnom vrednosti niza  ako i samo ako za svako 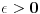 postoji... blah, blah, blah, blah
Malo snuzdeni pozdrav,
Marko
[ galet@world @ 06.04.2007. 08:16 ] @
Pobogu, Marko, zašto to toliko uzimaš k srcu, to nije toliko važno, ali, kao što si i sam rekao
zanimljivo jeste. To je samo moja intuitivna pobuna protiv nekih usvojenih stavova i zaista sam
zahvalan što uopšte raspravljaš o tome.
Moje eventualno neoprezne izjave, koje nisu baš "na note" ili zvuče preoštro ili čak uvredljivo
- ignoriši jer takve namere zaista nemam, a i zašto bih imao.
Evo jedne zanimljivosti:
Matematičari kažu da je a - a = a/∞ što ja nikako ne mogu da prihvatim.
Po mom mišljenju a - a je apsolutna nula koja označava nepostojanje i koja nema dimenziju,
međutim, a/∞ jeste nula, ali ta nula je drukčija - ona egzistira i ima onu dimenziju koju ima
veličina a
Na primer ja tvrdim da cos (a - b) ne postoji ako je a = b, jer je a - b nula
koja znači nepostojanje tj. nema ugla pa ne može biti ni kosinusa. Ta nula nema dimenziju ugla
izraženu u stepenima jer smo izrazom a - b uništili sve šta smo imali tj. nije ostala ni dimenzija
To je totalni prelaz na nepostojanje.
Sasvim je druga stvar ako kažemo da je cos 00 = 0
Ova nula koja ima dimenziju nije nastala oduzimanjem dveju jednakih veličina i kosinus takvog ugla
postoji jer postoji i ugao.
0 i ∞ su čudesni fenomeni. O tome sam hteo da nešto kažem ili pitam kad sam započeo ovu temu.
A o tome zaista ima šta da se kaže.
[ Daniel011 @ 06.04.2007. 08:55 ] @
Citat: galet@world: Na primer ja tvrdim da cos (a - b) ne postoji ako je a = b, jer je a - b nula
koja znači nepostojanje tj. nema ugla pa ne može biti ni kosinusa. Ta nula nema dimenziju ugla
izraženu u stepenima jer smo izrazom a - b uništili sve šta smo imali tj. nije ostala ni dimenzija
To je totalni prelaz na nepostojanje.
Sasvim je druga stvar ako kažemo da je cos 00 = 0
Ova nula koja ima dimenziju nije nastala oduzimanjem dveju jednakih veličina i kosinus takvog ugla
postoji jer postoji i ugao.
Da li bi mogao malo da pojasniš (i eventualno potkrepiš nekim dokazima) tvrdnju da je a - b (gde su a i b jednaki uglovi) nula bez dimenzija, a da je 00 - nula koja ima dimenziju? [ galet@world @ 06.04.2007. 11:45 ] @
Ja nisam matematičar pa se bojim da nećeš biti zadovoljan mojim odgovorom, ali
pokušaću:
dimenzija:
Ako podeliš neku duž na beskonačno mnogo delova dobićeš nulu koja ima dimenziju dužine
zato što od takvih delova obrnutim postupkom možeš opet sastaviti tu duž.
Ako ti delovi ne bi imali dimenziju dužine onda obrnutim postupkom ne bi mogli dobiti duž
jer se dimenzija dužine ne može dobiti ni iz čega.
nepostojanje:
Ako imaš nekoliko cvetova koji mirišu (neka im je, recimo, taj miris dimenzija), pa ako to cveće
pokloniš devojci - tebi nije ostalo ništa - čak ni miris!
Kad te neko, posle toga vidi, on ni po čemu ne može znati šta si imao pa sad više nemaš.
Ako si nešto što postoji poništio njegovom suprotnošću nikako se na osnovu rezultata tog poništavanja
ne može znati šta je postojalo pre toga
(ne - koliko, nego -šta)
[ Daniel011 @ 06.04.2007. 13:16 ] @
Nemoj misliti da su matematičari (bilo bi neskromno s moje strane da i sebe ubrojim u iste) toliko zatucani matematikom da ne mogu da razumeju i nematematičke pristupe.  Sa tvojim objašnjenjem dimenzije se potpuno slažem, ali ako sam te dobro razumeo, to objašnjenje bi trebalo da se odnosi na 00. Međutim, ko je uopšte i spomenuo da je 00 dobijen deljenjem nekog ugla konačne vrednosti na beskonačno mnogo uglova? 00 je tako kao što piše, čista nula, ni pozitivna ni negativna.
Što se tiče tvog drugog objašnjenja, iliti nepostojanja: ako baš krenemo filozofski da razmišljamo, uvek možemo postaviti pitanje da li a i b mogu biti baš potpuno identični, ili je uvek jedna od te dve vrednosti malo veća od one druge za neku vrlo, vrlo malu, pa ajd da kažem i, beskonačno malu vrednost. To se vrlo lako može ilustrovati i u tvom primeru sa cvećem. Kupiš cveće u cvećarnici, pokloniš ga devojci i kad te posle toga neko vidi, neće ni po čemu znati da si imao cveće. Međutim, ako te neki pas (a psi, kao što znaš, imaju dobar njuh), omiriše, on će itekako osetiti miris cveća. Znači da su neki molekuli tih cvetova ipak ostali na tebi, na tvojim rukama, što opet znači da devojci nisi poklonio sve molekule cveća koje si dobio u cvećarnici, nego su neki molekuli ostali i na tebi, tj. 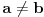 .
To je bio nematematički pristup. Evo i jednog matematičkog, u vezi tvrdnje da 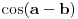 ne postoji ako je 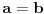 (i to ako je  ovog puta zaista, potpuno, jednako  :
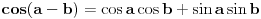 - ovu formulu sigurno znaš iz trigonometrije i sa njom se, pretpostavljam, slažeš.
Za 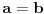 :
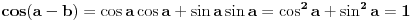
Možeš li pronaći u kom koraku ovog računa je načinjena greška, ukoliko je načinjena? [ galet@world @ 06.04.2007. 17:51 ] @
Citiram odgovor jednog matematičara:
"Ugao je u matematici oblast u ravni čiju granicu čine dve (zatvorene) poluprave sa zajedničkim temenom. Ako se uglovi mere u stepenima, onda ugao mora imati meru koja je veća od nule, a manja od 360. Ugao od nula stepeni ne postoji. Odgovarajuća prazna oblast se ne smatra uglom. Kosinus kao funkcija na uglovima se definiše kao funkcija koja uglovima pridružuje realne brojeve, pa shodno tome, kosinus ugla od nula stepeni ne postoji, jer takav ugao ne postoji. Sa druge strane, kosinus beskonačno malog ugla postoji, manji je od jedan i beskonačno blizak jedinici. No, o tome se može govoriti samo u svetlosti nearhimedovskih polja."
Što se tiče adicione teoreme, dakle, trebalo bi reći kada ona važi , a kada ne, odnosno funkcija kosinusa pridružuje realne brojeve uglovima koji postoje, a ne
uglu koji ne postoji. Dakle, ako se radi o grešci u računu - onda bi trebalo reći da taj račun ne važi ako su uglovi a i b jednaki.
[ Daniel011 @ 06.04.2007. 18:59 ] @
Da pitamo Wikipediu... Kaže ovako...
Citat: An angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle. Angles provide a means of expressing the difference in slope between two rays meeting at a vertex without the need to explicitly define the slopes of the two rays. Angles are studied in geometry and trigonometry.
Zatim dalje kaže:
Citat: Conventions on measurement
A positive (left) and a negative (right) angle.A convention universally adopted in mathematical writing is that angles given a sign are positive angles if measured counterclockwise, and negative angles if measured clockwise, from a given line. Ovime je rečeno da vrednost ugla može biti i manja od nule.
Citat: Some facts
...
An angle of 0° would be two rays, one on top of the other; this is equivalent to one ray.
Znači, ne kaže se da ugao od 0° ne postoji, kaže se samo da je on ekvivalentan jednom kraku.
http://en.wikipedia.org/wiki/Angle
Što se tiče definicije ugla koju si citirao, ne znam o kom matematičaru se radi, ali zaista prvi put čujem da je vrednost ugla ograničena na  . Negativni uglovi postoje, što se vidi i iz Wikipediinog objašnjenja, a definisane su i trigonometrijske operacije negativnih uglova, 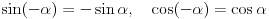 , a sinus i cosinus su takođe definisani i za uglove veće od 360°, pri čemu su i sinus i cosinus takvog ugla jednaki sinusu odnosno cosinusu ostatka tog ugla pri deljenju sa 360°, tj. 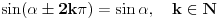 . [ mcetina2 @ 06.04.2007. 23:01 ] @
Uzeo sam malo temu k srcu jer zalim sto ne mogu da o njoj govorim na nacin na koji bi ti zeleo. Stavise, ne mogu o njoj da govorim na nacin na koji bi vecina ljudi zelela o njoj da govori.
Ti si dao lep primer bas za ovo. Citiram:
dimenzija:
Ako podeliš neku duž na beskonačno mnogo delova dobićeš nulu koja ima dimenziju dužine
zato što od takvih delova obrnutim postupkom možeš opet sastaviti tu duž.
Ako ti delovi ne bi imali dimenziju dužine onda obrnutim postupkom ne bi mogli dobiti duž
jer se dimenzija dužine ne može dobiti ni iz čega.
Problem je u tome sto u klasicnoj analizi nije moguce matematicki precizno pricati o nuli koju si ovde naveo. Ova beskonacno mala duz tj. ugao sa dimenzijom prosto nije dobro definisan. Definisane su samo konacne duzi/uglovi i nula duz (tacka) odnosno nula-ugao (poluprava).
Za dobru definiciju beskonacno malih velicina tj. tvoje nule sa dimenzijom ( 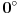 ), neophodno je razumeti nestandardnu analizu.
[ mcetina2 @ 06.04.2007. 23:18 ] @
galet, ukoliko u standardnoj analizi hoces da pricas o "beskonacno maloj duzi", to *moras* da uradis na sledeci nacin:
1) krenes od konacne duzi i nazoves je 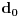
2) definises proces kojim tu duz delis na manje duzi. Onda proces ponovis k puta gde je k konacan prirodni broj. Na taj nacin dobijes sekvencu duzi 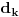
3) definises kriterijum/meru rastojanja izmedju duzi ove vrste. Drugim recima, definises pozitivno rastojanje 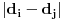
4) primetis da za dovoljno velike i i j ovo rastojanje, iako i dalje pozitivno, postaje proizvoljno malo. precizno receno, za svako pozitivno 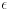 , postoji prirodan broj n tako da za sve i,j>n, 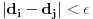 . Primeti da i dalje nema pomena o beskonacnim/beskonacno malim velicinama.
5) zakljucis da niz duzi koji si definisao tezi nekoj (za sada nepoznatoj) duzi takvom da za svako 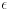 postoji prirodan broj n takav da za sve k>n, 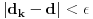 .
Onda samo na osnovu osobine 5) rezonujes o ovoj granicnoj duzi d. Zakljucis da je jedinstvena i, kada malo razmislis, vidis da je ova duz d u stvari nije duz vec pojedinacna tacka. Ali, ovo nije tvoja "beskonacno mala duz sa dimenzijom" od koje je moguce sastaviti pravu. To sigurno nije ni bilo koja od duzi 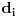 jer su sve veoma konacne duzine. Pa gde je onda ta tvoja duz?
Najpriblizniji odgovor je da se beskonacno mala duz 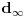 krije u samom procesu koji sam ovde opisao. 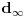 nije u pravom smislu reci ni duz ni tacka vec sam *proces* deljenja duzi.
Ako ovo zvuci cudno i komplikovano, to je zato sto jeste :)
Medjutim, Weirstrass-ovi granicni procesi su i izuzetno mocni. Na osnovu samo gorenavedene ideje moguce je matematicki precizno, samo na osnovu diskretnih prirodnih brojeva izgraditi citav koncept neprekidnosti/kontinuuma/realnih brojeva, granicnih vrednosti, izvoda, integrala, diferencijalnih jednacina, etc, etc... sve to bez "pozitivne nule" i "beskonacno malih delova sa dimenzijom" [ mcetina2 @ 06.04.2007. 23:25 ] @
Opet gledajuci diskusiju -- komentar --
a/∞ u standardnoj Weirstrass-ovoj analizi prosto nije definisano.... posledica nepostojanja beskonacno malih vrednosti u standardnoj analizi.
[ galet@world @ 07.04.2007. 13:34 ] @
@ Daniel011
Dve prave koje se seku imaju jednu zajedničku tačku koja je zajedničko teme četiri ugla.
Ta četiri ugla ispunjavaju uslove definicije:
"Ugao je u matematici oblast u ravni čiju granicu čine dve (zatvorene) poluprave sa zajedničkim temenom."
Međutim, definicija ugla od nula stepeni po Wikipediji ne ispunjava taj uslov, jer ako se prave poklope
onda su im sve tačke zajedničke pa bi taj ugao imao beskonačno mnogo temena.
S druge strane, kroz zajedničku tačku dveju pravih može se postaviti bezbroj pravih koje su paralelne sa nekom
trećom pravom. Ona dva manja ugla između bilo kojih od tih pravih imaju 00 i svi se međusobno
razlikuju. Te nule koje imaju dimenziju, međusobno se razlikuju.
@ mcetina2
Slažem se da je teško definisati beskonačno malu veličinu, ali opet mi se čini da to ne bi trebalo da znači da
se neka duž ne može podeliti na beskonačno mnogo delova.
Ne bih bih se složio na primer da se integraljenje može izvršiti bez sabiranja beskonačno mnogo
"beskonacno malih delova sa dimenzijom"
[ Daniel011 @ 07.04.2007. 15:21 ] @
Citat: galet@world: Dve prave koje se seku imaju jednu zajedničku tačku koja je zajedničko teme četiri ugla.
Ta četiri ugla ispunjavaju uslove definicije:
"Ugao je u matematici oblast u ravni čiju granicu čine dve (zatvorene) poluprave sa zajedničkim temenom."
Međutim, definicija ugla od nula stepeni po Wikipediji ne ispunjava taj uslov, jer ako se prave poklope
onda su im sve tačke zajedničke pa bi taj ugao imao beskonačno mnogo temena. Ako krenemo od definicije koju si uprao citirao, "Ugao je u matematici oblast u ravni čiju granicu čine dve (zatvorene) poluprave sa zajedničkim temenom", tj. da ugao formiraju poluprave a ne prave, tada nema nikakve dileme koja će tačka biti teme kod ugla od 0° - to će biti ona tačka kojom je svaka od ove dve poluprave (koje se u ovom slučaju poklapaju) ograničena s jedne strane.
Citat: galet@world: S druge strane, kroz zajedničku tačku dveju pravih može se postaviti bezbroj pravih koje su paralelne sa nekom trećom pravom. Kroz bilo koju tačku je moguće postaviti jednu i samo jednu pravu koja je paralelna sa nekom zadatom pravom. [ galet@world @ 07.04.2007. 20:01 ] @
Daniel011:
Citat: Ako krenemo od definicije koju si uprao citirao, "Ugao je u matematici oblast u ravni čiju granicu čine dve (zatvorene) poluprave sa zajedničkim temenom", tj. da ugao formiraju poluprave a ne prave, tada nema nikakve dileme koja će tačka biti teme kod ugla od 0° - to će biti ona tačka kojom je svaka od ove dve poluprave (koje se u ovom slučaju poklapaju) ograničena s jedne strane.
Taj ograničavajući kraj polupravih možeš da odsečeš u proizvoljno odabranoj dužini pa se neće ništa promeniti
izuzev što će druga tačka biti "teme". To, međutim, ne možeš učiniti kod uglova koji imaju dimenziju.
Citat: Kroz bilo koju tačku je moguće postaviti jednu i samo jednu pravu koja je paralelna sa nekom zadatom pravom.
To nije dokazano. S tim se Lobačevski ne bi složio
[ mcetina2 @ 08.04.2007. 02:51 ] @
I Riemann-ov i Lebesgue integral uvode se u standardnoj analizi upravo preko epsilon-delta definicije granicnog procesa koju sam ranije opisao.
U slucaju Riemann-ovog integrala, formira se beskonacan niz 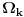 podela intervala x-ose [a,b] po kome se integrali. Pri tome kada k->infinity, duzina intervala od kojih se sastoji podela 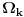 tezi nuli. Konkretno:
za svako 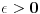 postoji n tako da za sve k>n, sve podele 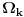 se sastoje od delica duzine manje od 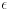 . Onda se posmatraju aproksimacije integralu 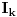 koje odgovaraju podelama 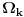 . Primeti se da ako je funkcija koja se integrali dovoljno regularna, vrednosti 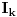 teze odredjenoj vrednosti (za svako epsilon postoji n tako da za svi i i j vece od n, 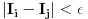 ....). Granicna vrednost I definisana ovim nizom naziva se vrednoscu integrala.
Galet, imam utisak da se i dalje nisi zamislio nad ovom epsilon-delta definicijom i potrudio da shvatis kako izbegava koriscenje beskonacno malih delova. Mozda je greska do mene jer bih ti kao nematematicaru mozda zaista trebao da nacrtam neku sliku, pogotovo oko ove definicije Riemann-ovog integrala.
Marko
[ galet@world @ 08.04.2007. 11:53 ] @
HRISTOS VOSKRESE !
Citat: mcetina2:
Galet, imam utisak da se i dalje nisi zamislio nad ovom epsilon-delta definicijom i potrudio da shvatis kako izbegava koriscenje beskonacno malih delova. Mozda je greska do mene jer bih ti kao nematematicaru mozda zaista trebao da nacrtam neku sliku, pogotovo oko ove definicije Riemann-ovog integrala.
Pa nacrtaj neku sliku, Marko, možda ćemo se razumeti. Evo, naprimer ovako:
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|