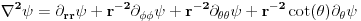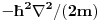
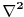
Pretpostavljas da mislis na kvantni Hamiltonijan. U tom slucaju treba ti operator p^2 odnosno tj sam u tvom omiljenom koordinatnom sistemu.

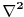
Tu puuuuno pomaze ako razmislis o tome sta u stvari geometrijski predstavlja.
Pa, geometrijski gledano, to je divergencija gradijenta. A divergencija je definisana cinjenicom da za svaku zapreminu V i vektorsko polje v u toj zapremini,


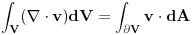
Ovo pak mozes da iskazes u raznim koordinatnim sistemima za elementarnu zapreminu dV u tom sistemu i na taj nacin sracunas divergenciju.

Ovde cu da predlozim jednu alternativu ovom postupku. Ono sto ti u kvantnoj u stvari treba su matricni elementi .
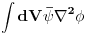
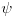
Ako su talasne funkcije i normalizovane, onda teze nuli u beskonacnosti. Stoga:
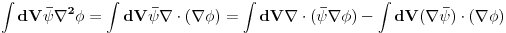
gde .

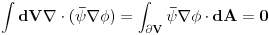
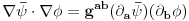
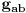
E, sad, u tvom omiljenom koordinatnom sistemu, gde je metricki tenzor u tom koordinatnom sistemu. Ako koordinate odaberes na iole razuman nacin, g ce biti dijagonalna matrica. Npr, u sfericnim kordinatama,


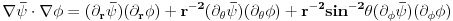
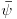
E, sad, istim postupkom kao gore, ali u tvom koordinatnom sistemu, prebacis vratis sve izvode na izvode . Npr., zapreminski integral drugug gorenavedenog clana transformises kao


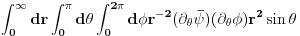
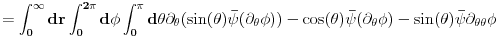
gde, posto ,

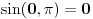
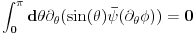
i gornji integral mozes da napises kao



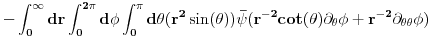
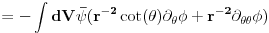
Slicnim postupkom iz treceg clana dobijes:

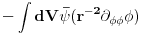
a iz prvog

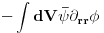
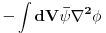
Poredjenjem ovog rezultata sa ocekivanim , u sfericnim koordinatama imas

Ovde sam pretpostavio da vec znas da je element zapremine u sfericnim koordinatama .
Takodje sam pretpostavio da umes da napises u tvom omiljenom koordinatnom sistemu. Ako te moje spominjanje metrike zbunjuje, potrazi ili razmisli malo o mom iskazu za ovu velicinu sam -- zaboravi na metriku i tenzore.

Jos par komentara o ovom izvodjenju. Neko "vican" diferencijalnoj geometriji rekao bi nesto u stilu:
Pa, prvo sracunas . To ti je vektorsko polje. Onda sracunas . Posto drugi izvod deluje na vektorsko polje, moramo da koristimo pravi izraz za kovarijantni izvod vektora u zadatim koordinatama. To obuhvata Christoffel-ove simbole koje onda moramo da sracunamo (). Na posletku kontraktujemo a i b indekse metrikom i dobijemo rezultat.

Bullshit, kazem ja. Divergencija vektorskog polja ima mnogo jasniju geometrijsku interpretaciju (zapreminski integral divergencije jednak je povrsinskom integralu vektora). A za ovu interpretaciju uopste *nije potreban* kovarijantni izvod, niti konekcija, niti Christoffel-ovi simboli -- potrebna je samo metrika! Zato ako nekoga pitas za rotor i divergenciju u proizvoljnim koordinatama (ili pak proizvodljno zakrivljenom prostoru!) i kada ti onda pocne pricu o Christoffelovim simbolima, ucutkaj ga :)

Speaking of curved spaces --
Procedura koju sam opisao za izracunavanje vazi u proizvoljno zakrivljenim prostorima bez modifikacije! Sve sto je potrebno je ubaciti odgovarajuci izraz za metriku odnosno za . Ovaj izraz ionako definise geometriju prostora -- a, preko navedenog izvodjenja, definise i prilicno jednostavno (Laplacijan).

Tako npr. za vezbu mozes da sracunas skalarnog polja u Schwarzschildovoj geometriji izvan nerotirajuce crne rupe. A cemu to sluzi.... e... to je dobro pitanje :)

End of rant--
Marko