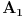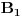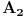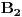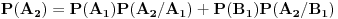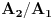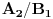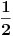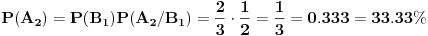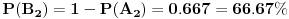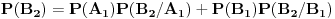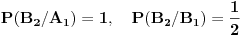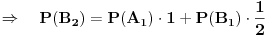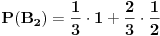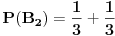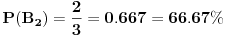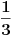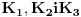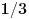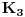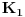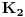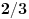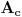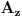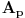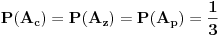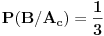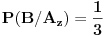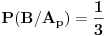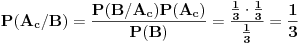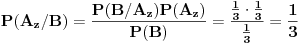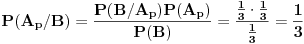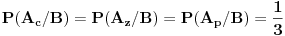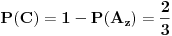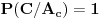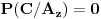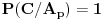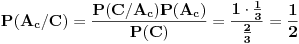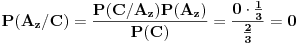|
|
[ marko1985 @ 30.03.2007. 17:09 ] @
|
| Ne spadam u napredne matematičare, možda čak ni u onu srednju klasu....svejedno molim za pomoć oko nečega što me muči danima. Evo o čemu se radi...
Pre neko veče neko društvo bilo kod mene....vidimo reklamu za onaj suludi PINK šou "Menjam ženu" i ono izvlačenje koverti. Ukoliko neko ne zna kako se te koverte izvlače evo kratkog objašnjenja: U 3 koverte se nalaze iznosi od 5, 45 i 150 k dinara. Prvo izvlači jedna žena (ima na raspologanju sve tri koverte), a potom i druga (na raspolaganju 2 preostale koverte).
I tako pola večeri smo se mi ganjali ko ima veće šanse, da bi se na kraju kao složili da su šanse podjednake, svi sem mene.
Moje pitanje je: KO IMA VIŠE ŠANSE DA IZVUČE VEĆU SUMU?
Ajde da probam ja da laički da obrazložim zašto ne mislim da su šanse iste. Znači nama je cilj KOVERTA SA NAJVEĆOM SUMOM. Da bi uprostili celu priču znači imamo dve koverte koje možemo da označimo sa B (koverte koje imaju manje sume) i jednu kovertu koja je A (najveća suma).
Prva žena koja bira ima 33,33 % šanse da izvuče kovertu A, tj. 66.66 % jednu od koverti B. Što znači da će u većini slučajeva izvući kovertu B. Druga žena je takođe imala neku kovertu "favorita" i takođe je imala šansu od 66.66 % da odabere kovertu B, sve dok prva žena nije izvukla kovertu. Pod pretpostavkom da je prva žena izvukla kovertu B, a da to nije ista koverta koju je druga žena "pikirala" onda se drugoj ženi znatno povećavaju šanse da izvuče kovertu A. Po meni, on bi u tom slučaju trebala da promeni svoju "favorit" kovertu i odluči se za onu drugu i tako bi joj šanse da izvuče kovertu A bile 66.66 %. Potrudiću se da malo objasnim i priču i oko te druge žene. Znači druga žena "favorizuje" jednu od 3 koverte i šansa da je "favorizovala" pogrešnu je 66.66 %. Kako je videla da je prva žena izvukla pogrešnu kovertu njoj se sužava izbor na 2 koverte. A kako je na početku "favorizovala" kovertu čija je šansa bila 33.33 % da je to koverta A, onda bi u to slučaju trebala da se odluči za onu drugu kovertu i time poveća verovatnoću da izvuče kovertu A.
E ja stvarno ne znam da li će ovo iko razumeti....ja bolje nisam mogao da objasnim. Ako neko kapira šta je pisac hteo da kaže neka mi otkloni dilemu da ne lupam glavom jer sigurno neću izmisliti novu teoremu, a možda mogu i poludeti :))))
Poydrav svima |
[ Daniel011 @ 30.03.2007. 17:34 ] @
Tvoje društvo je u pravu. 
Evo zašto: Ti sve vreme razmatraš slučaj da je prva žena izvukla kovertu na koju druga žena nije "pikirala" i da je to bila "pogrešna" koverta. Ali zanemaruješ druge moguće slučajeve, a jedan od njih je da je prva žena izvukla kovertu koju ova druga nije pikirala, a da je to bila prava koverta. Postoji još i slučaj da je prva žena izvukla kovertu koju je ova druga pikirala, pa onda dva podslučaja ovog slučaja, da je ta koverta bila "prava" ili "pogrešna". Sve te slučajeve moraš uzeti u razmatranje.
Ako idemo školskim putem, koristeći formule, verovatnoća da će druga žena izvući pravu kovertu može se izračunati na sledeći način:
Uvedemo sledeće oznake za događaje:
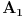 - prva žena je izvukla "pravu" kovertu;
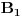 - prva žena je izvukla "pogrešnu" kovertu;
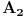 - druga žena je izvukla "pravu" kovertu;
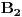 - druga žena je izvukla "pogrešnu" kovertu;
Zatim računamo verovatnoću za 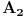 :
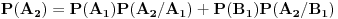
Objašnjenje: mogući ishodi prvog izvlačenja su 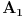 i 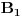 . Zbir verovatnoća ta dva događaja je  . Pošto verovatnoća ishoda drugog izvlačenja zavisi od ishoda prvog, on se računa po prethodnoj formuli. U toj formuli oznaka 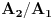 označava slučaj da se desio događaj 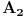 kada je prethodno ostvaren događaj 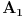 (u ovom slučaju 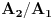 je očigledno nemoguć događaj, tj. verovatnoća mu je  , tako da prvi sabirak otpada), a 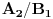 označava slučaj da se desio događaj 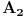 kada je prethodno ostvaren događaj 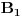 (verovatnoća događaja 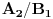 je 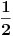 ).
Prema tome,
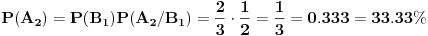
Odnosno, verovatnoća da će druga žena izvući "pogrešnu" kovertu:
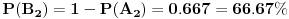
A može još i na ovaj način:
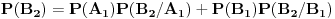
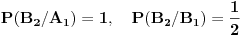
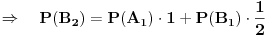
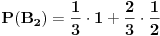
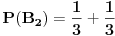
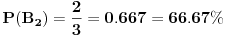 [Ovu poruku je menjao Daniel011 dana 31.03.2007. u 02:08 GMT+1]
[Ovu poruku je menjao Daniel011 dana 31.03.2007. u 02:08 GMT+1][ braker @ 31.03.2007. 01:28 ] @
Da,da.
Ako sam dobro razumeo point of view, mislim da si ti u pravu.:)
Ovako - nudish dvema osobama da izaberu po jednu od 3 ponudjene koverte, od kojih je samo jedna ona prava - i to tako shto prvo jedna od njih bira od ponudjene 3, a zatim ova druga od preostale 2.
E sada, pre nego shto izaberu koverte, ova druga osoba koja bira od preostale 2, kako ti kazhesh, ''pikira'' jednu kovertu josh dok su sve 3 ponudjene, tako da su im shanse u tom pochetnom trenutku (u vreme odluke, a pre samog izbora) podjednake - 1:3.
Ako prva osoba izabere kovertu koja nije ''pikirana'' od strane druge i nije ona prava, onda druga osoba treba da promeni izbor jer je veca verovatnoca da je ona druga (niti "pikirana", ni izabrana) prava.
P.S. Jel pala opklada na kraju:)
[ Daniel011 @ 31.03.2007. 01:38 ] @
Ne slažem se.
Štaviše, odgovorno tvrdim da takvo razmišljanje nije ispravno.
Dok su u igri bile sve 3 koverte, verovatnoća za svaku od njih da je baš ta koverta ona prava je 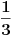 , to se slažemo.
Onog momenta kada iz igre ispadne jedna koverta i pokaže se da je ta koverta bila pogrešna, tada svakoj od one dve preostale koverte verovatnoća da je baš ta koverta prava "poraste" sa 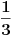 na 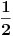 . Prema tome - i dalje je ista šansa za obe preostale koverte. [ Djomloun @ 31.03.2007. 01:45 ] @
Uhm koliko se ja secam verovatnoce (mada mi ona nije jacha strana;) postoje dva sluchaja:
--prvi, da svi izvlace istovremeno (sxto ovde nije sluchaj;) i onda svi imaju isto verovatnocu da izvuku masx kesxa tj 1/3 [broj povljnih ishoda/broj ishoda]
-drugi, kada se verovatnoca ishoda B (druga zxena izvlachi;) zavisi od verovatnoce ishoda A (prvo izvlachenje;) a rachnua se...uhm...pa ne znam napamet ali ako se dobro secam postavljaju se hipoteze:
I hipoteza verovatnoca da je A izvukla max
II -//- izvukla mid
III -//- izvukla min
...
i tako sve moguce kombinacije (hipoteze) pa se onda rachuna verovatnoca pojedinih ishoda.
[ Daniel011 @ 31.03.2007. 01:59 ] @
Da se malo nadovežem na objašnjenje koje je izneo braker.
Polazeći tom logikom, zašto ne bi mogao razmišljati i na sledeći način: druga žena u početku "pikira" jednu od 3 ponuđene koverte. I toj "pikiranoj" koverti, a i onim preostalim dvema kovertama, podjednake su šanse da je "ona prava" - 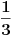 . Prva žena izvlači jednu od one dve koverte koja nije bila "pikirana" od strane druge žene. Ispostavlja se da je ta koverta "pogrešna". Na stolu su ostale dve koverte. Jedna je ona "pikirana", a druga nije. E ova koja nije, njoj je šansa u startu (kao i ostalima) bila 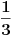 . Znači da tu kovertu ne treba izabirati, tj. zaključak je da druga žena treba da ostane pri svom prvobitnom izboru.
Naravno, ovo razmišljanje je takođe pogrešno - obe koverte posle izvlačenja prve (pogrešne) imaju istu šansu. Hteo sam ovime samo da pokažem da dato razmišljanje može da nas dovede do pogrešnih zaključaka.
Uostalom, ko ne veruje neka proveri zadatak experimentalno - ništa lakše nego skupiti 3 koverte, u jednu staviti nešto, npr. list hartije ili neku novčanicu kako bi to bila ona "prava" - i dogovoriti se sa još jednom osobom da jedno 50-tak puta obavite izvlačenja. Statistika će pokazati da je šansa uvek 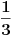 . [ braker @ 31.03.2007. 05:37 ] @
@Daniel
Mislim da greshish (ali dozvoljavam:) i da nisam u pravu).
Jednostavno nije moguce da imaju podjednake shanse, jer se tako problem svodi na istovremeno biranje jedne od tri ponudjene koverte, uz mogucnost biranja iste - a to je iskljucheno.
Ono shto meni predstavlja nepremostivu prepreku (uzrokovanu neznanjem), jeste implementacija intuitivne pretpostavke da ce promena fiktivnog izbora (aka "pikiranje") osobe koja druga bira, imati za posledicu vecu verovatnocu izbora prave koverte.
Hm, we'll see.
edit: Izgleda da je reshenje primena Bayesove formule.
Trenutno nemam vremena:)
[Ovu poruku je menjao braker dana 31.03.2007. u 08:17 GMT+1]
[ Nedeljko @ 31.03.2007. 08:20 ] @
Danijel011 je potpuno u pravu. Njegov račun je tačan. Ima i drugih načina da se dobije isti rezultat:
Neka je ai događaj da je i-ta žena izvukla pravu kovertu, a bi da je i-ta žena izvukla pogrešnu kovertu. Dakle, treba razmotriti verovatnoće sledećih 8 mogućnosti:
a1a2a3 : 0 (ne mogu sve tri izvući pravu kovertu),
a1a2b3 : 0 (ne mogu dve izvući pravu kovertu),
a1b2a3 : 0 (ne mogu dve izvući pravu kovertu),
a1b2b3 : 1/3 * 2/2 * 1/1 = 1/3,
b1a2a3 : 0 (ne mogu dve izvući pravu kovertu),
b1a2b3 : 2/3 * 1/2 * 1/1 = 1/3,
b1b2a3 : 2/3 * 1/2 * 1/1 = 1/3,
b1b2b3 : 0 (bar jedna mora izvući pravu kovertu),
Za prvu je povoljan četvti slučaj, za drugu šesti i za treću sedmi.
[ Daniel011 @ 31.03.2007. 09:17 ] @
@braker
To što imaju podjednake šanse, uopšte ne znači da se problem svodi na istovremeno biranje jedne od tri ponuđene koverte.
Sa druge strane, problem se lako može svesti na slučaj u kome prvo jedna žena bira kovertu, ali je ne otvara sve dok druga žena ne izabere neku od preostale dve koverte.
@Nedeljko
Slažem se i sa tvojim postupkom, tj. rezultat se može dobiti i na taj način, računanjem verovatnoće za svaki od članova skupa mogućih ishoda.
[ braker @ 31.03.2007. 10:15 ] @
Uh, ja i dalje ne kapiram, ali se nadam da nece predstavljati problem da primetim josh neshto.
Ovo je ono shto sam rekao i na chemu se moja tvrdnja temelji:
Citat: Ako prva osoba izabere kovertu koja nije ''pikirana'' od strane druge i nije ona prava, onda druga osoba treba da promeni izbor jer je veca verovatnoca da je ona druga (niti "pikirana", ni izabrana) prava.
Oznachimo koverte sa 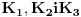
Verovatnoca da prva osoba izabere pravu kovertu je 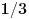 , i tu se slazhemo.
Recimo, da je izabrala kovertu 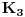 - ako je to prava to spada u predvidjenu 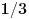 , medjutim ako to nije prava koverta, a druga osoba pikira kovertu 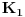 , onda u sluchaju promene izbora druge osobe - dakle posle ponovnog izbora koverte 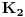 , verovatnoca prema Bayes-ovoj teoremi iznosi 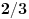
Da ushtedim texanje, lako se da uochiti analogija sa ovim zadatkom:
[ Daniel011 @ 31.03.2007. 10:27 ] @
Slučaj koji si naveo u attachmentu se bitno razlikuje od našeg slučaja.
U tvom zadatku je ključna rečenica " A presenter who knows what door the prize is behind, and who must open a door, but is not permitted to open the door we have pickked or the door with the prize...", a u našem zadatku to jednostavno nije slučaj, tj. žena koja prva bira kovertu niti zna koja je koverta "prava", niti zna koju kovertu druga žena "pikira".
(Reč "pickked" sam morao da napišem sa dva "k", jer ako je napišem samo sa jednim "k", softver je prepozna kao izvesnu srpsku reč, pa je cenzuriše.  ) [ braker @ 31.03.2007. 10:39 ] @
Daniel
Hajde molim te prochitaj citat u mom prethodnom postu (da ne citiram vishe sam sebe:))- verovatno cesh zakljuchiti da se radi o istim uslovima.
I postavljach teme je to isto naveo.
[ Daniel011 @ 31.03.2007. 10:48 ] @
Ako misliš na ovaj citat,
Citat: braker: Ako prva osoba izabere kovertu koja nije ''pikirana'' od strane druge i nije ona prava, onda druga osoba treba da promeni izbor jer je veca verovatnoca da je ona druga (niti "pikirana", ni izabrana) prava.
njega sam vrlo dobro pročitao i sa njim se ne slažem.
Postavljač teme je jasno naveo uslove da žena koja prva izvlači koverat ima šansu 1:3 da izvuče pravi koverat, što znači da ona ne zna koji je koverat "pravi".
Ili, posmatraj ovako. Stavi se u poziciju druge žene, tj. da pikiraš neki od tri koverata. Kolika je verovatnoća da će prva žena izvući koverat koji nisi pikirao? Verovatnoća je 2:3. A kolika je verovatnoća u tvom zadatku da će voditelj otvoriti ona vrata koja nisi izabrao? Verovatnoća je 1, odnosno 100%, jer je tako dužan da uradi prema pravilima. A sve to suštinski menja dalji način razmišljanja pri računanju verovatnoće odabira prave koverte, odnosno pravih vrata. [ braker @ 31.03.2007. 12:04 ] @
Mislim upravo na taj citat, i posmatrao sam problem iskljuchivo pod uslovom da prva osoba uzima koverat koji nije ''pikiran'' od strane druge, shto sam u prvom postu i naveo, a shodno ovom:
Citat: marko1985:Pod pretpostavkom da je prva žena izvukla kovertu B, a da to nije ista koverta koju je druga žena "pikirala" onda se drugoj ženi znatno povećavaju šanse da izvuče kovertu A.
I kada sam rekao da greshish, mislio sam na ovo:
Citat: Daniel011: Da se malo nadovežem na objašnjenje koje je izneo braker.
Polazeći tom logikom, zašto ne bi mogao razmišljati i na sledeći način: druga žena u početku "pikira" jednu od 3 ponuđene koverte. I toj "pikiranoj" koverti, a i onim preostalim dvema kovertama, podjednake su šanse da je "ona prava" - 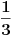 . Prva žena izvlači jednu od one dve koverte koja nije bila "pikirana" od strane druge žene. Ispostavlja se da je ta koverta "pogrešna". Na stolu su ostale dve koverte. Jedna je ona "pikirana", a druga nije. E ova koja nije, njoj je šansa u startu (kao i ostalima) bila 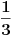 . Znači da tu kovertu ne treba izabirati, tj. zaključak je da druga žena treba da ostane pri svom prvobitnom izboru.
Tvoje reshenje bez ovog dodatnog uslova nisam (i ne bih:)) dovodio u pitanje.
Svejedno, meni je koristilo:)
best regards
braker
[Ovu poruku je menjao braker dana 31.03.2007. u 13:16 GMT+1][ marko1985 @ 31.03.2007. 14:59 ] @
u jeeeeeeeee.....nisam očekivao ovakvu debatu !
i sinoć sam se bavio ovom temom sa nekim poznanicima, i mislim da je priča sledeća...(kako stvari stoje izgleda da je tako) !
Tačno je da su pojedinačne šanse i prvoj i drugoj osobi 1/3 !
Ali je takođe ispravno razmišljanje da ako je prva osoba izvukla pogrešnu kovertu, a to nije ona koju je druga "pikirala", onda drugoj osobi ostaju 2 koverte, i ukoliko promeni svoj izbor ima duplo više šanse da izvuče dobitnu kovertu. Opet je to samo verovatnoća , i to ne mora biti tako....
ja sam samo razmišljao o situaciji kada će prva izabrati pogrešnu kovertu, ili da će izabrati "pikiranu" tako da je tu moja greška....razmatrao sam samo ono što je meni odgovaralo :)
Čak smo pokušali i eksperimentalno da ovo dokažemo na sledeći način : Uzeo sam total commander i obrisao *.key kako više ne bi bio registrovan. I onda vas na početku čeka da stisnete jedan od ponuđenih brojeva da biste ušli u program. Naravno samo je jedan pravi....Izveli smo to 100 puta (bože koliko smo samo opterećeni ovim problemom). Rezultat je išao u korist ove priča koju sam ispričao, ali opet mislim da to ipak nije nešto na šta bi se moglo 100 % osloniti !
[ ventura @ 31.03.2007. 15:12 ] @
Citat: marko1985:
Moje pitanje je: KO IMA VIŠE ŠANSE DA IZVUČE VEĆU SUMU?
Najveću šansu da izvuče kovertu sa 150k dinara, je onaj ko dečku koji sprema koverte plati 500 evra :)
Tu vam nikakva druga matematika neće pomoći ;)
[ Daniel011 @ 31.03.2007. 15:12 ] @
Citat: marko1985: Ali je takođe ispravno razmišljanje da ako je prva osoba izvukla pogrešnu kovertu, a to nije ona koju je druga "pikirala", onda drugoj osobi ostaju 2 koverte, i ukoliko promeni svoj izbor ima duplo više šanse da izvuče dobitnu kovertu.
Ljudi, ja ne znam kojim više argumentima da vam dokažem da to nije tačno.
Pokušaću još na ovaj način, pa ako ni to ne uspe, onda znači ili da ne čitate moje postove, ili...
Neka su 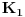 , 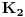 i 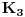 date koverte od kojih je "pogrešna" 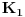 i "pogrešna" je još jedna, nebitno koja. Druga žena pikira 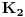 , a prva žena izvlači 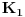 i konstatuje da je 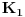 pogrešna. I sada, po tom rezonu, druga žena bi trebalo da promeni svoj izbor i da ovaj put izabere 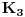 .
Ali druga žena je sa podjednakom verovatnoćom u startu mogla da pikira i 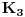 , pa da posle izvlačenja 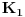 koja je pogrešna, prema istom rezonu, promeni izbor tako da na kraju izvuče 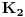 . Shvatate li koliko je to razmišljanje pogrešno?
Dajem sebi slobodu da kažem da onaj ko razmišlja na taj način nije u pravu, jer ovde se ne radi o političkoj diskusiji gde svako može i da bude i da ne bude u pravu, gde ima više stavova i gde svaki treba uvažavati, nego se ovde radi o matematici koja je egzaktna nauka i u kojoj se sve može dokazati i opovrgnuti, a ja sam do sada bar na tri načina opovrgao taj pogrešan način razmišljanja koji ovde pokušava da se nametne.
[Ovu poruku je menjao Daniel011 dana 31.03.2007. u 17:09 GMT+1][ optix @ 31.03.2007. 17:05 ] @
Malo mi je naporno da ispratim sta je ko sve rekao, ali dacu svoje vidjenje ovog malo izmenjenog Monty Hall problema pa kome pomogne, pomogne...
Logika da se promenom izbora uvecavaju sanse za pogodak "prave" koverte je ispravna samo pod sledecim uslovima:
1. Da je u dovoljnoj meri moguce kvantifikovati odluku (pikiranje) za jednu kovertu. Ovo znaci da se onaj ko bira unapred jasno odluci (makar i u glavi) za jednu od ponudjenih koverti. Ili u originalnom M.H. problemu za jedna od tri ponudjenih vrata. Brze i ceste promene misljenja samo pogorsavaju verovatnoce, i komplikuju matematiku... Ovo bas i nije lako za razmatranje jer iskljucuje mogucnost dvoumljenja i troumljenja sto je naravno cest slucaj sa svakim ljudskim bicem.
2. Da se nakon tog izbora, jedno pogresno resenje otkrije onome ko bira.
Dodatni uslov koji vazi za ovaj ovde problem sa kovertama, je da se osoba koja druga bira kovertu ne opredeli za kovertu koju ce izabrati prva osoba. U originalnom M.H problemu, ovo ne moze biti slucaj, jer za koja god vrata da se osoba odluci, jedno od pogresnih resenja ce mu biti predstavljeno. Zasto je ovo ovde bitno? Pa ukoliko se i druga osoba opredelila za kovertu koju je prva izabrala, onda ne moze doci do promene izbora. Naprotiv, onda dolazi do samo jednog izbora, izmedju preostale dve koverte i za to su sanse 50-50, ukoliko prva zena nije izabrala pravu kovertu.
Akko (ako i samo ako!) su ovi uslovi ispunjeni, ispravno je promeniti odluku, tj. ona druga koverta ili vrata imaju vise sanse da budu ispravne.
Dokaz za ovo je vec napisan, ako je nekome lakse, moze i ovako da se iskaze:
Kolika je verovatnoca da pogresimo ukoliko promenimo odluku nakon sto nam je jedno od neispravnih resenja predstavljeno? Jasno je da cemo pogresiti samo ukoliko smo se iz prve odlucili za ispravnu kovertu. Verovatnoca da smo ispravno pogodili kovertu ili vrata u prvoj odluci je 33%. Dakle 66% je verovatnoca da necemo pogresiti prilikom promene izbora.
Pozdrav.
P.S. Ako dodjete u situaciju da na Pinku izvlacite koverte, Venturino resenje je najbolje ;) [ Daniel011 @ 31.03.2007. 17:24 ] @
Evo još jednog dokaza da menjanje odluke ne uvećava šansu za odabir prave koverte. Ovog puta sam dokaz izveo koristeći pomenutu Bayes-ovu formulu, na taj način što sam zadatak sa crvenim, zelenim i plavim vratima, koji je Braker postavio u attachmentu, preveo i prepravio tako da odgovara ovom našem slučaju sa kovertama. Izmene su bile neminovne, s obzirom da početni uslovi u ova dva zadatka, iako na prvi pogled deluju identični, ipak to nisu.
Na raspolaganju su tri koverte - crvena, zelena i plava - od kojih jedna u sebi sadrži nagradu. Izabiramo crvenu kovertu. Žena koja prva izvlači kovertu i pri tom ne zna u kojoj koverti je nagrada, kao što ne zna ni koju smo kovertu mi izabrali, izvlači zelenu kovertu. Pod pretpostavkom da u toj koverti nema nagrade, koja je verovatnoća da je nagrada u plavoj koverti?
Nazovimo situaciju u kojoj je nagrada u datoj koverti 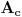 , 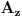 , 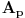 . (c-crvena, z-zelena, p-plava)
Za početak, 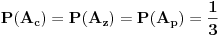 i, kako bismo uprostili stvari, pretpostavimo da smo već u mislima izabrali ("pikirali") crvenu kovertu.
Nazovimo  "prva žena izvlači zelenu kovertu". Bez ikakvog prethodnog znanja, ovom događaju pridružujemo vrednost verovatnoće 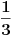 .
- u situaciji da je nagrada u crvenoj koverti, prva žena izvlači crvenu, zelenu ili plavu kovertu, po slučajnom izboru. Dakle, 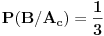
- u situaciji da je nagrada u zelenoj koverti, prva žena izvlači crvenu, zelenu ili plavu kovertu, po slučajnom izboru. Dakle, 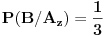
- u situaciji da je nagrada u plavoj koverti, prva žena izvlači crvenu, zelenu ili plavu kovertu, po slučajnom izboru. Dakle, 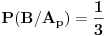
Dakle,
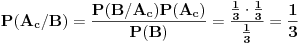
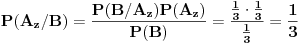
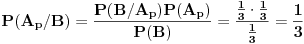
To bi bila "prepravka" attachovanog zadatka sa vratima, tako da odgovara našem slučaju sa kovertama. Kao što se vidi, ništa posebno ovime nije dokazano. Pokazano je samo to, da je posle izvlačenja zelene koverte od strane prve žene, ali pre otvaranja te zelene koverte, verovatnoća da je nagrada u bilo kojoj od koverata, ista za sve tri koverte i iznosi 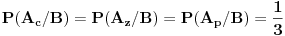 .
Zatim dalje proširujemo postupak: sada kad je poznato da je prva žena izvukla zelenu kovertu, tj. da više nije neizvesno koju će kovertu ona izvući, uvodimo događaj da se u toj zelenoj koverti ne nalazi nagrada, tj. da prva žena ostaje bez nagrade i taj događaj nazovemo  . Očigledno je da je
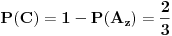
- u situaciji da je nagrada u crvenoj koverti, prva žena izvlačenjem zelene koverte 100% ostaje bez nagrade. Dakle, 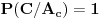
- u situaciji da je nagrada u zelenoj koverti, prva žena izvlačenjem zelene koverte nikako ne može ostati bez nagrade. Dakle, 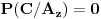
- u situaciji da je nagrada u plavoj koverti, prva žena izvlačenjem zelene koverte 100% ostaje bez nagrade. Dakle, 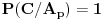
Dakle,
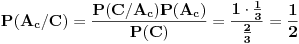
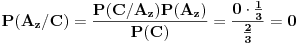
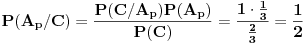 Zaključak: kada se desio događaj
Zaključak: kada se desio događaj  , tj. prva žena izvukla zelenu kovertu, otvorila je i konstatovala da se u njoj ne nalazi nagrada, verovatnoće , tj. prva žena izvukla zelenu kovertu, otvorila je i konstatovala da se u njoj ne nalazi nagrada, verovatnoće 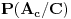 i i 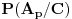 da je nagrada u crvenoj, odnosno plavoj koverti, su jednake i iznose da je nagrada u crvenoj, odnosno plavoj koverti, su jednake i iznose 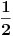 . .[ Daniel011 @ 31.03.2007. 17:40 ] @
Citat: optix: Dodatni uslov koji vazi za ovaj ovde problem sa kovertama, je da se osoba koja druga bira kovertu ne opredeli za kovertu koju ce izabrati prva osoba. U originalnom M.H problemu, ovo ne moze biti slucaj, jer za koja god vrata da se osoba odluci, jedno od pogresnih resenja ce mu biti predstavljeno. Zasto je ovo ovde bitno? Pa ukoliko se i druga osoba opredelila za kovertu koju je prva izabrala, onda ne moze doci do promene izbora. Naprotiv, onda dolazi do samo jednog izbora, izmedju preostale dve koverte
Sa ovim se apsolutno slažem i to zapravo i jeste suština. Upravo sam to i pokušao da objasnim u jednom od prethodnih postova. [ braker @ 31.03.2007. 20:53 ] @
Citat: marko1985Ali je takođe ispravno razmišljanje da ako je prva osoba izvukla pogrešnu kovertu, a to nije ona koju je druga "pikirala", onda drugoj osobi ostaju 2 koverte, i ukoliko promeni svoj izbor ima duplo više šanse da izvuče dobitnu kovertu. Opet je to samo verovatnoća , i to ne mora biti tako.... Citat: Daniel011: Ljudi, ja ne znam kojim više argumentima da vam dokažem da to nije tačno.
Pokušaću još na ovaj način, pa ako ni to ne uspe, onda znači ili da ne čitate moje postove, ili...
Daniel, sa dosta pazhnje chitam tvoje postove i slazhem se sa nachinom pristupa diskusiji, ipak je ovo matematika:)
Medjutim, pod ovim uslovima koje je marko naveo, tvoja tvrdnja nije tachna!
Polazish od pogreshnih pretpostavki.
Onog trenutka kada prva osoba izvuche prvu kovertu koja nije parava i nije ''pikirana'' od strane druge, prestaje da biva predmetom nasheg interesovanja!
U tom sluchaju sledece postaje relevantno za razmatranje problema:
-Koju je kovertu izvukla prva osoba (koja nije prava)
-Preostale dve koverte (i verovatnoca vezana za njih)
-Prvobitni izbor druge osobe i promena odluke
Ako znamo da koverta koju je izvukla prva osoba nije prava i ako to nije ona koju je druga pikirala, onda se promenom izbora druge osobe njene shanse udvostruchuju.Ovo je teza koju zastupam od prvog posta na ovoj temi.
Ovo se i dokazuje primenom Bayes-ove formule.
optix je imao identichan pristup.
Na OVOM linku je to lepo i slikovito prikazano.Treba samo obratiti pazhnju na pochetne uslove.
Verovatnoce za preostale 2 koverte (pod navedenim uslovima) nisu jednake.
Kako bilo, ovim se moje ucheshce na ovoj temi zavrshava.
Pozdrav.
[ Daniel011 @ 31.03.2007. 21:47 ] @
Braker, na osnovu tvojih ranijih postova na ovom forumu (van ove teme) vidim da zaista dobro barataš matematikom i tim pre ne mogu da shvatim da na ovoj temi praviš ovakve elementarne greške.
Link koji si dao u prethodnom postu predstavlja slučaj identičan onom sa vratima. A ja sam već napisao u jednom postu (da si zaista čitao moje postove kao što kažeš da jesi, pročitao bi i to) da se slučaj sa vratima i naš slučaj sa kovertama ne mogu porediti. U slučaju sa kovertama, izbor prve osobe nikako ne zavisi od onoga šta je druga osoba u svojim mislima odlučila da izvuče (sem ako nisu u telepatskoj vezi, ali takav slučaj ne razmatramo), a u slučaju sa vratima, kao i u ovom slučaju sa portalima, koja će nam vrata, tj. portal biti otvoreni i prikazani da su pogrešni, to zavisi od toga koji smo izbor napravili. Zar je tako teško shvatiti tu razliku?
Poslednje što bih želeo to je da zvučim cinično. Ali zaista ne mogu a da ti ne postavim pitanje, jesi li ti imao verovatnoću u srednjoj školi i/ili na fakultetu, bilo kao poseban predmet, bilo kao oblast u sklopu matematike? Ako si imao, da li su predavali o zavisnim i nezavisnim događajima? Ako nisu, onda je to ozbiljan propust. Ako pak jesu, onda molim te da praviš razliku između ta dva pojma. U zadatku sa vratima/portalima su u pitanju međusobno zavisni događaji, a u našem zadatku sa kovertama - međusobno nezavisni događaji.
Pošto se pozivaš na Bayes-ovu formulu pri dokazivanju da se posle promene izbora vrata/portala šansa za odabir ispravnih vrata/portala udvostručava, slobodno možeš pogledati moj pretprošli post (koji ti je verovatno promakao), u kome sam upravo primenom Bayes-ove formule dokazao da se šansa za izbor ispravne koverte, posle promene odluke, ne menja.
[Ovu poruku je menjao Daniel011 dana 01.04.2007. u 17:06 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|