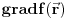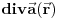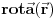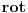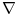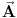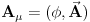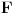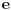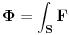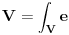Da bi bilo potpuno jasno o čemu se radi i prilikom ručnog pisanja na papiru, tabli i sličnom, kao i prilikom ispisa u elektronskim verzijama, mislim da je sasvim korektno pisati grad, div i rot običnim (nemasnim) slovima, a ostale veličine u skladu sa uobičajenim oznakama funkcija i vektora:
,
i
.
Iz definicija ovih prostornih izvoda je jasno koji od njih je vektor a koji skalar.

Što se tiče nula vektora, koliko je meni poznato, pravilno je pisati ga i kao 0 i kao 0, jer čim je nula, znači da ionako nema ni intenzitet, ni pravac, ni smer, tj. nema nijednu od vektorskih osobina.
Isto kao što se u fizici za brzinu nekog tela ne može pisati v=10, nego se mora napisati ili v=10m/s ili v=10km/h ili v=10km/s ili... ali se za telo koje miruje može napisati da mu je v=0, mada nije greška ni v=0m/s, ali se taj m/s ionako množi sa nulom, što opet daje samo nulu...

Masna slova valjda prvenstveno koristimo da ne bi bilo zabune.

Npr. grad v gde je v skalar je sam vektor dok je grad v gde je v vektor tenzor. Stavise, ovaj vektorski grad je u krivolinijskim koordinatama mnogo zapetljaniji od ovog skalarnog. Zato je bitno v pisati masnim slovima. Sa druge strane rot i div mogu da deluju samo na vektore pa moze da se kaze da u rot v/div v nije neophodno v pisati masnim slovima.

Medjutim, lep je coding practice da se svi vektori pisu masno. Na taj nacin citalac o odredjenim velicinama odmah razmislja na pravi nacin (pravac, smer, itd.), kao sto je Daniel011 rekao. Sto se nula vektora medjutim tice, isto kao sto je Daniel011 rekao, ne verujem da vecinu citalaca zanima pravac i smer :) Zato je po meni OK da se nula vektor pise ne-masnim slovima.

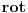
Sto se masnih oznaka za div/grad/rot tice, prvo da kazem da obicne TeX italic oznake tipa *puno* idu na nerve. div/grad/rot, ako je ikako moguce, treba barem pisati u text-modu unutar TeX-u matematickih izraza. Tako barem lice na operatore a ne na proizvod promenjljivih.

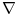
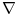
Sto se boldovanja istih tice, mislim da to potice od boldovanja (covariant derivative) kao vektorskog operatora koji od skalara pravi vektore, od vektora tenzore, etc. Medjutim, ovo bas i nema puno smisla jer ne postoji ne-vektorski , div/rot. Zato bih ja ove operatore pisao ne-masno ali u text ili TeX keyword modu.

Jos par licnih komentara.

Meni strelice dosta idu na zivce. Nekako puno kite i saraju iskaze i zato mnoogo vise volim boldovanje vektora. Nazalost, \bf{v} ne radi na ovom forumu(*) i zato u mojim postovima svi vektori izgledaju kao skalari :(

Strelice koristim samo ako hocu da naglasim da je neka velicina 3-vektor a ne ko/kontravarijantnog vektor u 4D. Npr. vs. .

Kad smo vec kod index-notacije.... Cim se uvede Einstein-ova index konvencija, na osnovu pozicije indexa za svaku velicinu se odmah vidi o cemu se radi (vektor, skalar, forma, tenzor, etc.). Zato se velicine sa indexima nikada ne bolduju. Ako se u diferencijalnoj geometriji neka velicina bolduje, to obicno znaci da autor naglasava da ista velicina ima neku veoma odredjenu geometrijsku interpretaciju. Npr., uobicajeno je da se diferencijalne forme kao npr. Maxwell tenzor ili zapreminski element bolduju a onda prirodno koriste kao i (nema dA odnosno dV jer F odnosno e vec to sadrze u sebi!)

(*) proverih malopre -- izgleda da sada radi :))) To znaci da cu ubuduce morati da se potrudim da boldujem vektore.