U vezi 1. zadatka, očigledno je da je tvoje rešenje tačno, a da je ono rešenje koje piše u knjizi netačno. To možeš i proveriti tako što i jedno i drugo rešenje uvrstiš u polaznu jednačinu:



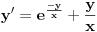
Za tvoje rešenje se dobija:



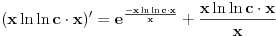
i kad se to sredi, dobije se da je jednakost tačna.

Za rešenje iz knjige, ne dobija se tačna jednakost.

U knjizi su malo pobrkali lonchice ;)

[att_img]


P.S. I moja Mathematica 5.2 kazxe isto ;)

E da... Proveri da kojim slučajem u postavci 1. zadatka ne piše , znači bez onog minusa u eksponentu, jer bi u tom slučaju rešenje iz knjige bilo tačno.

ma nije bas knjiga vec proslogodisnji rokovi iz matike 2 :D

uglavnom postavka je ispravna (s minusom) a ponudjena rjesenja su:
1.
2.
3.
4.
i nase peto:

Hvala na brzom odazivu ;)

Imal ko ideju o 2. pitanju ?

Pa onda je tachan odgovor pod 1.

ln(c*x)=lnc+lnx=C+lnx

C je neka nova constanta ;)

Slažem se. ;)

Da al umjesto može stajati i svejedno ;)

Evo Cypher u vezi sa j-nom totalnog diferencijala.

P(x,y)dx+Q(x,y)dy=0

Hvala, mnogo! tek sam sad vidio odgovor na temu :S:S:S moze lock!