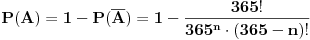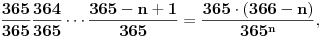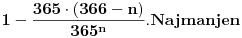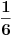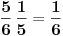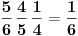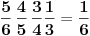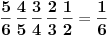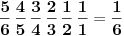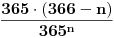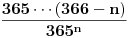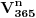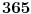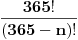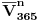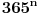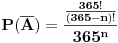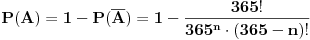1. Pretpostavićemo da niko nije rođen 29. februara. Verovatnoća da u društvu od osoba svi imaju različite rođendane je pa je tražena verovatnoća za koje je ova verovatnoća veća od 0.5 je 24.

2. Verovatnoća da iz prvog puta pogodi je .
Verovatnoća da iz drugog puta pogodi je .
Verovatnoća da iz trećeg puta pogodi je .
Verovatnoća da iz četvrtog puta pogodi je .
Verovatnoća da iz petog puta pogodi je .
Verovatnoća da iz šestog puta pogodi je .

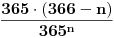
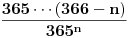
Slažem se sa oba Nedeljkova rešenja, s tim da u prvom zadatku umesto izraza treba da stoji . Očigledno je u pitanju samo omaška u kucanju (jedno izostavljeno slovo u TeX-u), ali bolje da na to ukažem, da ne bi došlo do nepotrebnog zbunjivanja.

Ja sam prvi zadatak rešavao na drugi način, korišćenjem varijacija bez ponavljanja i sa ponavljanjem. Isto kao i Nedeljko, računao sam prvo verovatnoću komplementarnog događaja, da nijedna od osoba nije rođena istog datuma, a zatim dobijenu verovatnoću oduzimam od jedinice i time dobijam traženu verovatnoću.

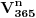
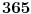
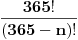
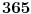
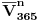
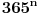
Broj povoljnih slučajeva (tj. slučajeva da su sve osobe rođene različitih datuma) jednak je , odnosno broj varijacija od elemenata klase bez ponavljanja i on iznosi . Broj mogućih (ukupnih) slučajeva predstavlja varijaciju od elemenata klase sa ponavljanjem, tj. , a to iznosi . Verovatnoća da od osoba nijedna nije rođena istog dana u godini predstavlja količnik broja povoljnih i broja mogućih događaja, tj. .

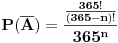
Tražena verovatnoća je, prema tome,