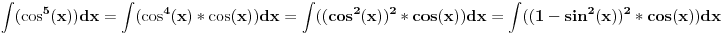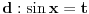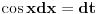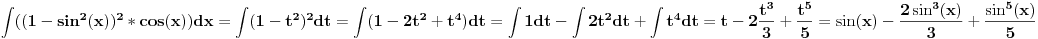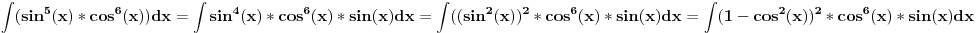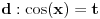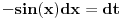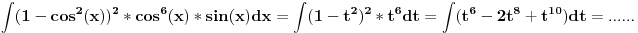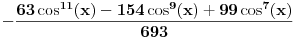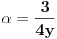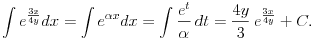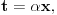[ jhondoe @ 05.04.2007. 17:55 ] @
|
| Rješavam integrale za ispit i najteže mi je integrirati ove integrale
1. cos^5[x]dx ako pokušam supstituciju cos(x)=t rješenje je cos^6[x]/6*sin[x], a to nije točno kaže matematica
2. sin^5[x]*cos^6[x]dx, znam svodi se na supstituciju sa ponavljanjem dok se ne ukine sin funkcija, ima li ko neki plan
3. e^(3x/4y), dx y je konstanta (ovo je iz dvostrukog integrala)
bio bi zahvalan na objašnjenju kako se ovo integrira jer potencije donekle kužim, ali ovo ne uspjevam razbiti.
hvala. |
[ mcetina2 @ 05.04.2007. 18:16 ] @
cos^5(x) dx -> cos^4(x) d(sin x) -> (1-sin^2(x))^2 d(sin x) -> (1-y^2)^2 dy -> (y^4 - 2y^2 + 1) dy ->
y^5/5 - 2y^3/3 + y gde y = sin(x). Mathematica checks out.
sin^5(x) cos^6(x) -> -cos^6(x) sin^4(x) d(cos(x)) -> -y^6 (1-y^2)^2 dy -> ...
e^(3x/4y) dx -> e^(3x/4y) 4y/3 d(3x/4y) -> 4y/3 e^z dz -> 4y/3 e^z, z = 3x/4y
[ braker @ 05.04.2007. 21:41 ] @
[ RMAN @ 06.04.2007. 02:59 ] @
Evo,da i ja probam.
1.
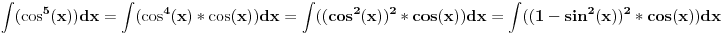
Sad smena:
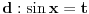
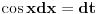
Pa onda imamo:
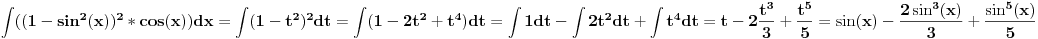
2.
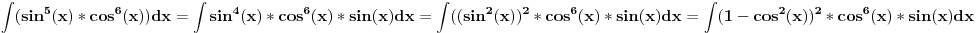
Sad smena:
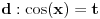
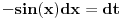
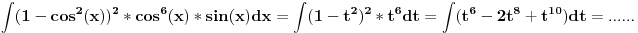
Dalje su tablicni.
Krajnji rezultat je(trebalo bi da je dobar):
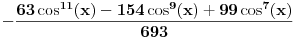
3.
Za sad nemam ideju kako bi ovaj resio ali ako provalim javicu
 [Ovu poruku je menjao RMAN dana 06.04.2007. u 10:44 GMT+1]
[Ovu poruku je menjao RMAN dana 06.04.2007. u 10:44 GMT+1][ jhondoe @ 06.04.2007. 07:02 ] @
Hvala kod prvog ja sam cos^4 [x] mjenjao sa (1+cos(2x))^2 zato i nisam mogao dobiti rješenje. Hvala.
[ Nedeljko @ 06.04.2007. 10:45 ] @
Za
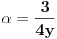
imamo
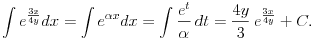
Korišćena je smena
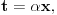
kao i činjenica da

ne zavisi od

po kome se vrši integracija.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.