[ KoKuZ @ 05.04.2007. 19:48 ] @
| pozdravljam.. na ispitu sam imao funkciju y=1+1/ln(x-1) da li neko moze da mi uradio ovu funkciju jer ne znam gdje grijesim... govorim o 7 koraka to jest analiza funkcije hvala unaprijed.... |
|
[ KoKuZ @ 05.04.2007. 19:48 ] @
[ RMAN @ 05.04.2007. 22:58 ] @
Pa da probam.....
Znaci funkcija je: 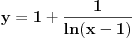 1.Domen 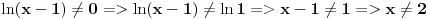   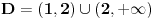 2.Nule: 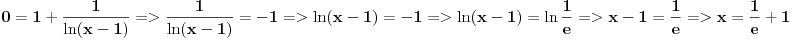 Znaci nula funkcije je u tacki: 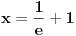 3.Znak Spojimo datu funkciju pod jedan razlomak: 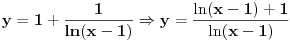 Sada znak funkcije zavisi od funkcija 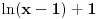 i i 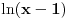 Nacrtamo te dve funkcije i trazimo kada im je isti znak. Dobije se: 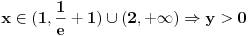  4.Asimptote Vertikalna je 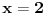 -Prvo prilazimo broju 2 sa desne strane npr. 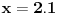 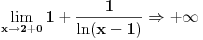 Odavde se vidi da funkcija,kada se priblizava broju 2 sa desne strane,tezi u Odavde se vidi da funkcija,kada se priblizava broju 2 sa desne strane,tezi u  -Sada prilazimo broju 2 sa leve strane npr. 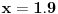 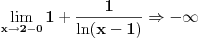 Odavde se vidi da funkcija,kada se priblizava broju 2 sa leve strane,tezi u Odavde se vidi da funkcija,kada se priblizava broju 2 sa leve strane,tezi u  Horizontalna asimptota: Pustimo da x tezi beskonacno( 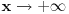 ) )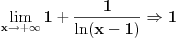 Znaci da je horizontalna asimptota  Ostalo je jos da x pustimo da tezi 1 ( 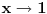 ) )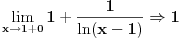 Znaci kada prilazimo broju 1 sa desne strane(sa leve ne moze jer je van domena) funkcija tezi u 1. 5.Monotonost Kad se sredi prvi izvod funkcije dobije se: 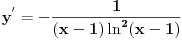 Prvi izvod je uvek negativan sto znaci da funkcija na celom svom toku opada. 6.Konveksnost(prevojne tacke) Ako sam dobro uradio drugi izvod je: 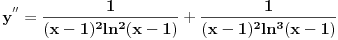 Drugi izvod je uvek pozitivan sto znaci da funkcija nema prevojnih tacaka odnosno konveksna je nadole. Uf,konacno! Evo kako funkcija treba da izgleda: [att_img] [Ovu poruku je menjao RMAN dana 06.04.2007. u 03:16 GMT+1] [ mcetina2 @ 06.04.2007. 05:32 ] @
> govorim o 7 koraka to jest analiza funkcije
a onda: > domen, nule, znak, H asimptota, V asimptota, monotonost, konveksnost Moja namera nije da nipodostavam veoma lep gorenavedeni odgovor na postavljeno pitanje. Medjutim.... Da li nekog osim mene zabrinjava cinjenica da kada neko spomene "analizu funkcije", gomila drugih odmah zna da nabroji (istih) 7 koraka? Mislim, sta je to toliko sveto u bas tih 7 koraka da ih svi trebamo primeniti cim vidimo neku funkciju? To mislim osim deklaracije odredjenih profesora na odredjenim katedrama? Sta ce da bude ako posle resavanja gomile problema sa tih 7 koraka student naidje na funkciju tipa: y(x) = 1 ako je x raciconalan y(x) = 0 ako je x iracionalan ili pak, y(x) koje potice od nekog fizickog procesa (Lotka-Volterra predator-prey model) za koje jedan ili vise koraka ovog procesa ne daju smislene ili lake odgovore? Drugim recima, ako su trenirani po sablonu, kako ce studenti da primene matematiku na nove probleme na koje naidju? P.S. Razumem da ljudi traze pomoc za ispite na gorenavedenim katedrama.... medjutim, ipak me zabrinjava ova neinventivnost u ucenju matematike i fizike. upravo zbog ovoga kada god mogu pokusavam da ponudim odgovore na pitanja koji pospesuju neku radoznalost. [ Daniel011 @ 06.04.2007. 13:49 ] @
Slažem se sa svakom kritikom ako je kreativna, a po meni, da bi neka kritika bila kreativna, mora ponuditi neki metod rešavanja problema, alternativan onom metodu koji je predmet kritike.
Zato očekujem da ponudiš svoj metod analiziranja i crtanja grafika date funkcije, a koji je bolji od ovde primenjenog u 7 koraka. Takođe, očekujem da ponudiš i svoj metod analiziranja, kao i crtanja grafika funkcije koju si spomenuo: 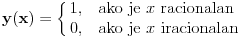 Ja, priznajem, nemam nikakvu ideju kako bih ovu funkciju i analizirao, a kamoli nacrtao njen grafik. [offtopic] Vidim da se danas funkcija svuda ispituje pomoću 7 koraka, mada smo mi u srednjoj školi to radili pomoću 11 koraka (dodatna četiri koraka su: parnost-neparnost, periodičnost, extremne vrednosti (max i min) i prevojne tačke su rađene u posebnom koraku). No, nebitno. [/offtopic] [ Kolins Balaban @ 06.04.2007. 14:16 ] @
Mislim da je sasvim nebitno u koliko ce se koraka ispitivati funkcija. bitno je da se ona ispita i da se dobiju potrebne informacije da se ona i nacrta. Svako radi to na svoj nacin, i svi su ok ;)
moj bi bio sljedeci: 1. Definiciono podrucje 2. Nule funkcije, znak funkcije 3. Simetrija (parnost,neparnost), periodicnost 4. Asimptote funkcije 5. Extremi funkcije (prvi izvod i njegove nule, drugi izvod i njegove nule----->min,max,prevojne tacke) 6. Monotonost funkcije (znak prvog izvoda, rast i opadanje funkcije) 7. Grafik funkcije Mislim da je to sasvim dovoljno da se funkcija nacrta, ali sve zavisi od slucaja do slucaja. Konkavnost i konvexnost se vidi iz extrema, i mislim da nema potrebe da se to isputuje u posebnoj tacki. Pozz [ Daniel011 @ 06.04.2007. 14:25 ] @
Nebitno, slažem se. Upravo to sam gore i napisao.
[ mcetina2 @ 06.04.2007. 20:11 ] @
Bitno je da se funkcija intuitivno razume kao i da se razume na koji nacin ta funkcija moze da se koristi.
Po meni, glavni problem sa gorenavedenom analizom je da je relativno proste funkcije danas veoma lako nacrtati na racunaru ili cak digitronu. Na osnovu ovog crteza, moguce je veoma brzo steci osecaj za dosta osobina funkcije poput nula, ekstremnih vrednosti i konvenksnosti. Za druge matematicke osobine funkcije poput definicionog podrucija medjutim racunari ne pomazu i zato na njih treba obratiti vise paznje. Pri tome razumem da je veoma zgodno da ako imas prostu funkciju znas da je brzo ispitas i na osnovu toga nacrtas (ili zamislis) bez racunara. Stavise, prvi bih rekao da ova sposobnost puno pomaze u intuitivnom razmisljanju o problemima. Medjutim, cim krenes da ispisujes izvode na par linija i resavas kvadratne jednacine gubis ovu intuitivnu prednost i time vreme. Zato bih rekao, inspirisan fizikom i pomoci racunara u njoj: 1. definiciono podrucije i moguca produzenja 2. periodicnost, parnost, druge simetrije 3. glatkost (kontinualna, postojanje prvog izvoda, postojanje drugog izvoda) (ako funkcija nije kontinualna, integrabilnost) 4. analiticko produzenje na kompleksne brojeve? ako da, nule, polovi i branch cuts 5. asimptote 6. globalne ekstremne vrednosti a tek onda, moguce uz pomoc racunara: 6. lokalne ekstremne vrednosti. znak drugog izvoda odnosno sopstvenih vrednosti matrice drugog izvoda na lokaciji ekstrema 7. nule 8. konveksnost/konkavnost 9. prevojne tacke ******************** Sto se funkcije racionalan-iracionalan tice: 1. Definisana na R bez ociglednog produzenja na C (sta cemo sa sqrt(2) + I?) 2. Parna. Periodicna sa bilo kojim racionalnim periodom (barem). 3. Ne-kontinualnu u svojoj bilo kojoj tacki (u bilo kojoj epsilon-okolini bilo kog racionalnog broja postoji iracionalan broj i obrnuto). Zato asimptote, analiticko produzenje i lokalne ekstremne vrednosti ne postoje. Nije Riemann-integrabilna ali jeste Lebesgue integrabilna (vidi "nule"). 7. Funkcija je ne-nula samo u svim racionalnim tackama cija ja Lebesgue mera pak 0. Sa stanovista Lebesgue integracije funkcija je ekvivalentna f(x)===1 i mozemo je integraliti. 8. Ni konveksna ni konkavna na bilo kom intervalu (iracionalan + iracionalan moze da bude i iracionalan i racionalan). 9. 0 i 1 racunar ne pomaze uopste. Sto se resenja diferencijalne jednacine tice, 1. nas vec tera da se zapitamo kako se diferencijalna jednacina ponasa. Konkretno, da li posle konacnog vremena resenje tezi beskonacnosti ili prestaje da postoji iz nekog drugog razloga 2. nas navodi da razmislimo o simetrijama same jednacine a onda i simetrijama generlnog resenja (koje mogu da budu manje ali da poticu od simetrija jednacine!) 3. nas navodi da analiziramo glatkost diferencijalne jednacine. Onda postoje teoreme koje nam govore o glatkosti resenja. Ako je resenje potpuno glatko, jednacina ce imati kompleksno produzenje. ovo pak moze da nam da jaku intuiciju o singularitetima resenja na koje mozemo da naidjemo ... [Ovu poruku je menjao mcetina2 dana 06.04.2007. u 23:47 GMT+1] [ Daniel011 @ 07.04.2007. 01:14 ] @
Ih, Marko, ja očekivao ti ćeš sad da uvedeš revolucionarno nov metod u ispitivanju funkcija, a ti samo malo promenio redosled koraka iz standardnog postupka...
[ Nedeljko @ 07.04.2007. 21:31 ] @
Ako je na nekom skupu
 izvod diferencijabilne funkcije negativan, to neznači da je ta funkcija opadajuća na tom skupu. To će svakako biti tačno ako je skup izvod diferencijabilne funkcije negativan, to neznači da je ta funkcija opadajuća na tom skupu. To će svakako biti tačno ako je skup  interval, ali ne i u opštem slučaju. interval, ali ne i u opštem slučaju.Definicija: Realna funkcija  definisana na nekom skupu definisana na nekom skupu 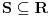 je monotono opadajuća na skupu je monotono opadajuća na skupu  ako za sve ako za sve 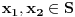 za koje je za koje je  važi važi 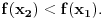 Teorema: Uz simboliku iz prethodne definicije, ako je 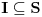 interval i funkcija interval i funkcija  je diferencijabilna na intervalu je diferencijabilna na intervalu  i i 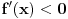 za sve za sve 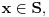 onda je funkcija onda je funkcija  monotono opadajuća na intervalu monotono opadajuća na intervalu 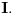 Napomena: Ako je na nekom skupu  izvod diferencijabilne funkcije negativan, to neznači da je ta funkcija opadajuća na tom skupu. To će svakako biti tačno ako je skup izvod diferencijabilne funkcije negativan, to neznači da je ta funkcija opadajuća na tom skupu. To će svakako biti tačno ako je skup  interval, ali ne i u opštem slučaju. interval, ali ne i u opštem slučaju.Primer: Funkcija 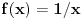 je definisana na skupu je definisana na skupu 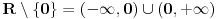 diferencijabilna je na celom svom domenu i izvod joj je na celom domenu negativan, ali nije na celom svom domenu monotono opadajuća, jer je diferencijabilna je na celom svom domenu i izvod joj je na celom domenu negativan, ali nije na celom svom domenu monotono opadajuća, jer je 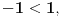 ali nije ali nije 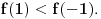 Ona je zapravo monotono opadajuća na intervalu Ona je zapravo monotono opadajuća na intervalu 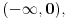 kao i na intervalu kao i na intervalu 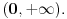 Citat: RMAN: 5.Monotonost Kad se sredi prvi izvod funkcije dobije se: 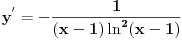 Prvi izvod je uvek negativan sto znaci da funkcija na celom svom toku opada. Data funkcija nije monotona na celom svom domenu (što se vidi i sa grafika), već na intervalima 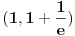 i i 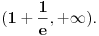 [ RMAN @ 08.04.2007. 03:12 ] @
@Nedeljko
Na razumem sta si hteo da kazes? Mislim da ocigledno je da funkcija na celom svom toku opada ,ili mozda gresim? [ Nedeljko @ 08.04.2007. 10:43 ] @
Data funkcija nije monotono opadajuća na celom svom domenu. Recimo,
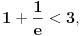 ali nije ali nije 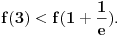 (Pročitaj definiciju.) Sa druge strane, (Pročitaj definiciju.) Sa druge strane,1) Funkcija monotono opada na intervalu 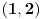 jer za ma koje jer za ma koje 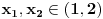 za koje je za koje je  važi važi 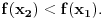 2) Funkcija monotono opada na intervalu 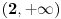 jer za ma koje jer za ma koje 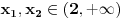 za koje je za koje je  važi važi 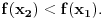 Međutim, to ne znači da je ona opadajuća (štaviše i nije) na skupu 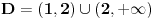 jer postoje jer postoje 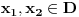 za koje nije za koje nije 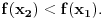 Primer sam već dao: Primer sam već dao: 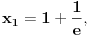 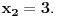 Od tačke Od tačke 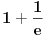 do tačke do tačke  funkcija je "porasla". To je moguće i pored negativnosti izvoda na celom domenu zato što između tačaka funkcija je "porasla". To je moguće i pored negativnosti izvoda na celom domenu zato što između tačaka 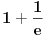 i i  postoji tačka u kojoj funkcija nije definisana. postoji tačka u kojoj funkcija nije definisana.Na intervalima sadržanim u domenu funkcije to ne može da se desi i upravo se na njima može zaključivati o monotoniji na osnovu izvoda. [ RMAN @ 08.04.2007. 23:10 ] @
U pravu si. Hvala!
[ ercegovac @ 25.06.2007. 14:43 ] @
Neka mi neko precizno objasni razliku izmedju 3 operatora
dx , "delta" x i "obrnuta devetka" x . Hvala [ Daniel011 @ 25.06.2007. 15:00 ] @
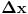 predstavlja razliku između predstavlja razliku između  i nekog njemu vrlo bliskog broja i nekog njemu vrlo bliskog broja  . Znači, . Znači, 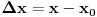 i to je vrlo mala veličina. i to je vrlo mala veličina.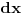 se dobija kada se dobija kada 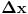 teži nuli, odnosno to je beskonačno mali priraštaj promenljive teži nuli, odnosno to je beskonačno mali priraštaj promenljive  . .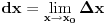 . .Izvod funkcije je zapravo količnik diferencijala te funkcije i diferencijala nezavisne promenljive: 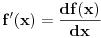 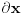 se upotrebljava kad imamo funkciju više promenljivih, pa tražimo njen izvod samo po se upotrebljava kad imamo funkciju više promenljivih, pa tražimo njen izvod samo po  : : 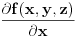 [ lilly_23 @ 30.03.2009. 16:11 ] @
nema sanse da ja odradim ovu funkciju,sva se popetljam............ak mozes da mi je uradis,zauvijek bi ti bila zahvalna
x*/2 puta lnx/2 rijecima:x na kvadrat kroz 2 puta ln x kroz 2 svih 7 koraka,s crtanjem i sve........molim te da pomognes [ Kolins Balaban @ 31.03.2009. 08:36 ] @
hajde ti reci gdje si tacno zapela, pa cemo pomoci. ako si zapela na svih 7 koraka, onda to nije dobro nikako i kad bi ti neko ovdje uradio taj zadatak (zadacu) to ti ne bi mnogo pomoglo. potrudi se (dok nije dosao bojan :) ) da nam pokazes da si bar pokusala ali je negdje zapelo i ne ide dalje. kuckanje u texu nije bas lako.
[ lilly_23 @ 31.03.2009. 21:58 ] @
znam teoretski sve,sto se tice postupka,kako se ide i sve to
fazon je sto mi ide s obicnim,prostim funkcijama,ali cim ln uleti i ono sto odradim sumnjam u njegovu tacnostt..... valja mi nac instruktora da mi to pojasni..............vjezbam,slomi se vjezbajuci,al dzaba kad mi nema ko pojasnit..... hitno mi treba rjesenje ovog zadatka,u frci sam s ocjenama,inace ne trazim lagan izlaz vani....al mi je sad potrebno [ Kolins Balaban @ 02.04.2009. 15:06 ] @
pa eto kolega RMAN je extra dobro objasnio postupak, samo sto je druga funkcija. ako ti odatle ne mozes skontati kako to primjeniti na tvoju funkciju, i pored toga sto jako dobro znas teoriju, onda ti samo instruktor moze pomoci. uostalom, ovo i nije tako teska fcja za nacrati. mislim da je ljenost u pitanju.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|