Upotrebiš smenu

pa integral postaje



Dalje probaj sam, pa javi kad i ako zapneš.

Hajd da ja probam ovako iz glave:


malo transformisemo podintegralnu funkciju na sljedeci ancin


Prema tome imamo da je

odnosno
gdje je



Prvi integral je tablicni, odnosno

a drugi rjesavamo parcijalnom integracijom stavljajuci da je:



odakle je


ovaj integral rjesavamo smjenom

pa je

odnosno

sada je

i na kraju


valjda je to TO. Pozz

PS: ako se dobro sjecam, ovaj integral bi se mogao rijesiti i smjenom - Euler-ova smjena.

Sorry sto sam te naveo na pogresan put, malo sam se zeznuo, ipak bi trebala smjena *
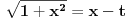
Kvadriranjem prethodne jednakosti, dobijemo da je

**
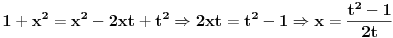
diferenciranjem dobijemo da je

***

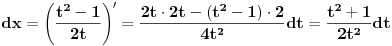
Iz jednakosti * koristenjem jednakosti ** dobijemo da je

****

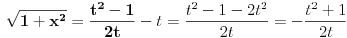
Kad jednakosti *** i **** vratimo u pocetni integral, dobijemo



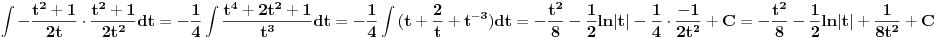
Iz jednakosti * dobijemo da je

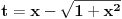
Vracanjem smjene, dobijemo:






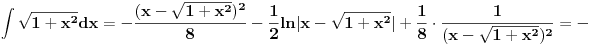
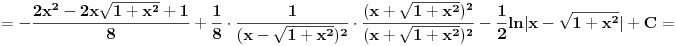
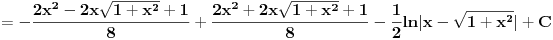
Kad se posljednji izraz malo sredi, dobije se



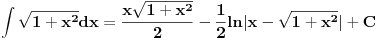_{[Ovu poruku je menjao Kolins Balaban dana 13.04.2007. u 00:25 GMT+1]}