Za ODE prvog reda uzeo bih samo vremenski invarijantnu jednacinu tipa y'(t) = f(y(t)) gde je f zadata funkcija.

Razlog je to sto vremenski promnjljivu jednacinu tipa y'(t) = f(y(t),t) mozes da napises kao sistem
[y, t]'(u) = [f(y,t), 1]
kao sto jednacine biseg reda mozes da napises kao sistem
[y y' y''...y^(n) t]'(u) = [y' y'' y'''.... y^(n) f(y,y',y''...y^(n),t) 1]

Drugim recima, svaku ODE mozes da napises kao vremenski invarijantan sistem nekog reda. Onda je za mene jednacina prvog reda akko je njen ekvivalentan vremenski invarijantan sistem prvog reda.

U ovom slucaju, ponasanje jednacine odredjeno je cisto funkcijom f(y) i u stvari, prilicno je dosadno.

f(y) ce imati odredjeni broj nula. Svaka od tih nula bice nepomicna tacka jednacine. Ako se malo pomeris od takve nule, ili se vracas ka njoj (stabilna nula) ili bezis od nje (nestabilna). Ako za y>y1 i y<y2 nema vise nula, onda sistem za y(t=0) > y1 moze ili da padne u y1 ili da ode u beskonacnost u konacnom ili beskonacnom vremenu. Slicno za y2.

Ovo je jako kratko ali se nadam da navodi diskusiju u zanimljivom smeru -- ne pitati za eksplicitno resenje vec prvo razumeti koje sve vrste dinamike data ODE moze da ima.

Marko

A bez veze i pricam --

Jednacinu y'(t) = f(y) moguce je lako resiti
dy/dt = f(y) =>
dy/f(y) = dt /integralis


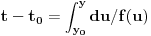
Naravno, ako pitas za sistem tipa y'(t) = f(y,t) (koji bi ja nazvao sistem drugog reda), imas vise opcija.
Odmah padaju na pamet linearne jednacine tipa y'(t) = A y + f(t) i Riccati-jeva jednacina....

Pokusavam da se setim jos necega ali ..... ova vrsta jednacine je malo neobicna sa stanovista fizike. Dinamicki sistemi su uvek barem drugog reda sto se izvoda funkcije tice. Tek onda mogu da budu i vremenski promenjljivi (sto ih po mojoj definiciji cini sistemima treceg reda).

Nisam siguran da sam razumeo na shta ciljash.
Da li zhelish da naglasish neophodnost postojanja nezavisno promenljive velichine kao dodatnog uslova da bi smo mogli razumeti stanje neke pojave opisane funkcijom, ili se pak radi o teoremi egzistencije i jedinstvenosti?

> Dinamicki sistemi su uvek barem drugog reda sto se izvoda funkcije tice. Tek onda mogu da budu i vremenski promenjljivi (sto ih po mojoj definiciji cini sistemima treceg reda).

Ciljam na prirodne pojave. Cak i najjednostavnije pojave su skoro uvek opisane jednacinom sa dve zavisne promenjljive (x(t) i p(t)) tipa [x p]'(t) = f(x,p). Ako na sistem deluje fiksna spoljna sila, to postaje [x p]'(t) = f(x,p,t). Ovo je posledica koriscenja Newton-ovog drugog zakona ili pak varijacionog principa / Hamiltonovih jednacina.

Eliminacija p, x ili neke kombinacije da bi se dobila jednacina tipa y'(t) = f(y,t) ponekad je moguca usled posebne simetrije problema. Medjutim, ne mogu odmah da se setim ni jednog primera.