[ petarm @ 14.04.2007. 23:01 ] @
| Voleo bih da mi neko objasni zasto je izvod Hevisajdove f-je delta f-ja i koji je njen znacaj. |
|
[ petarm @ 14.04.2007. 23:01 ] @
[ mcetina2 @ 15.04.2007. 00:02 ] @
Hint:
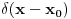 nije funkcija. Medjutim, nije funkcija. Medjutim, 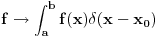 jeste dobro definisan linearni operator za dovoljno glatke funkcije f(x). Ako hoces da budes matematicki precizan, treba pricati o ovom operatoru a ne o samoj delta-"funkciji". jeste dobro definisan linearni operator za dovoljno glatke funkcije f(x). Ako hoces da budes matematicki precizan, treba pricati o ovom operatoru a ne o samoj delta-"funkciji".Stvari poput delta "funkcije" koje smisla imaju samo pod znakom integrala u analizi su poznate kao distribucije. Veoma su korisne za opis diskontinuiteta, singulariteta i tako toga.... [ Milan Milosevic @ 15.04.2007. 06:58 ] @
Kad funkcija trpi konacan skok u nekoj tacki tad njen prvi izvod trpi beskonacan skok.
To se moze objasniti najprostije preko same definicije izvoda H'(x)=dH(x)/dx. Ovde mozemo dx=x2-x1 posto ovde dx tezi nuli, a 1/0 tezi beskonacno, te je odavde i H'(0)=beskonacno, a u ostalom delu prostora po definiciji izvoda iz konstante nula. To i jeste definicije dirakove delta funkcije. [ Fitopatolog @ 15.04.2007. 21:54 ] @
Delta f-ja spada u generalisane (tzv nesvojstvene) f-je koje nisu f-je u pravom smislu (reč je o familiji f-ja) zato što:
može imati bilo koju vrednost u intervalu (-w,w), gde w->0, van tog intervala vrednost je nula, a inetgral (površina ispod krive) u tom intervalu mora biti 1. Hevisajdova f-ja pripada istoj kategoriji f-ja, pri čemu je: vrednost f-je jednaka 0 od -beskonačno do -w od -w do w vrednost nije strogo definisana (w->0), ali vazi H(x)=integral od -w do x (D(t) dt) vrednost f-je je 1 posle w [ petarm @ 18.04.2007. 08:13 ] @
A zasto je kod Hevisajdove f-je vrednost u 0 bas 1/2? I da li tako to tretiraju i matematicari ili oni Hevisajdovoj f-ji daju recimo vrednost 0 u 0?
[ Fitopatolog @ 18.04.2007. 22:15 ] @
To je anomalija Laplasove (Furijeove?) transformacije. Napravi Furijeovu transformaciju f-je H(t) pa potraži inverznu - u tom slučaju će ti se pojaviti da je Hinv(0)=1/2. Po definiciji H(t) za t=0 nije striktno ograničeno na 1/2, važi definicija iz mog prethodnog posta.
pogledaj http://mathworld.wolfram.com/HeavisideStepFunction.html deo pri dnu strane koji se odnosi na Furijeovu transformaciju Hevisajdove f-je. Uz Delta-funkciju je član 1/2, koji će pri inverznoj transformaciji dati vrednost 1/2 u nuli. [Ovu poruku je menjao Fitopatolog dana 18.04.2007. u 23:26 GMT+1] [ Fitopatolog @ 19.04.2007. 22:07 ] @
Evo i nešto preciznijeg odgovora:
Pošto H(t) (Hevisajdova ili odskočna f-ja) ne zadovoljava Dirihleov uslov ne može da ima Furijeovu transformaciju, bar ne u nekom "normalnom" obliku. Da bi se ipak došlo do Furijeove transformacije H(t) pribegava se triku: Traži se Furijeova transformacija f-je h(t)=H(t)-H(t-T), što je u stvari impuls širine T. h(t) ima Furijeovu transformaciju: F(h(t))=(1-exp(-j*w*T))/(j*w) a ako se pusti da T teži beskonačnosti impuls se pretvara u Hevisajdovu f-ju, pa se dobija sledeći izraz za Furijeovu transformaciju: H(w)=pi*D(w) + 1/(j*w) D je Dirakova f-ja. Inverzna Furijeova transformacija od H(w) će ponovo dati vrednost h(t), ali će član pi*D(w) dati vrednost 1/2 za t=0. Literatura: Ilija Stojanović: Osnovi Telekomunikacija, Građevinska knjiga 1977, strana 190-192 [ petarm @ 25.04.2007. 08:54 ] @
Ja sam cuo od jednog profesora da se to 1/2 uvodi zbog Fermi - Dirakove statistike.
[ Fitopatolog @ 25.04.2007. 19:58 ] @
Kakve tegobe ima rečena statistika ako se ne uvede ova 1/2?
[ Fitopatolog @ 30.04.2007. 20:14 ] @
Takođe je interesantan i Gibsov fenomen, videti:
http://mathworld.wolfram.com/GibbsPhenomenon.html http://en.wikipedia.org/wiki/Gibbs_phenomenon [ petarm @ 15.05.2007. 09:48 ] @
Ne znam to bih i ja voleo da znam. Verovatno nije zbog teskoca nego zbog bolje fizicke interpretacije.
[ Nedeljko @ 15.05.2007. 16:25 ] @
Citat: mcetina2: Hint: 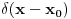 nije funkcija. Medjutim, nije funkcija. Medjutim, 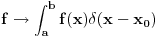 jeste dobro definisan linearni operator za dovoljno glatke funkcije f(x). jeste dobro definisan linearni operator za dovoljno glatke funkcije f(x).Nije mi baš najjasnije kako može biti dobro definisan integral nečega što nije dobro definisano. No, pustimo sad to. Sa 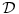 označimo skup svih beskonačno diferencijabilnih funkcija označimo skup svih beskonačno diferencijabilnih funkcija 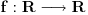 takvih da je skup takvih da je skup 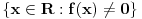 ograničen. Elemente skupa ograničen. Elemente skupa 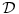 zovemo osnovnim funkcijama. zovemo osnovnim funkcijama.Za proizvoljne realne funkcije  definisane na istom domenu definisane na istom domenu  i proizvoljne realne konstante i proizvoljne realne konstante  pod funkcijom pod funkcijom  podrazumevaćemo funkciju podrazumevaćemo funkciju  definisanu jednakošću definisanu jednakošću 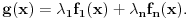 U tom slučaju, funkciju U tom slučaju, funkciju  zovemo i jednom linhearnom kombinacijom funkcija zovemo i jednom linhearnom kombinacijom funkcija  Skup 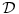 obrazuje vektorski prostor, što znači da je linearna kombinacija funkcija iz tog skupa takođe u tom skupu. Pod linearnim funkcionalom podrazumevaćemo preslikavanje obrazuje vektorski prostor, što znači da je linearna kombinacija funkcija iz tog skupa takođe u tom skupu. Pod linearnim funkcionalom podrazumevaćemo preslikavanje 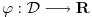 za koje je za koje je 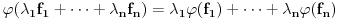 za ma koje za ma koje 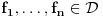 i i 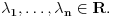 Za niz funkcija 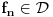 ćemo reći da konvergira ka funkciji ćemo reći da konvergira ka funkciji 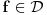 kada kada  teži beskonačnosti i pisaćemo teži beskonačnosti i pisaćemo 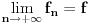 ako postoji ograničen skup ako postoji ograničen skup 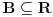 takav da je takav da je 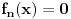 za svako za svako  i i 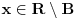 i ako za svaki prirodan broj i ako za svaki prirodan broj  i svako i svako  postoji prirodan broj postoji prirodan broj  takav da za svako takav da za svako 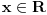 i svako i svako 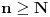 važi važi 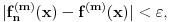 gde gde 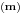 označava označava  -ti izvod date funkcije. -ti izvod date funkcije.Za niz realnih brojeva  ćemo reći da konvergira ka realnom broju ćemo reći da konvergira ka realnom broju  kada kada  teži beskonačnosti i pisaćemo teži beskonačnosti i pisaćemo 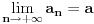 ako za svako ako za svako  postoji prirodan broj postoji prirodan broj  takav da za svako takav da za svako 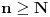 važi važi 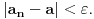 Pod distribucijom podrazumevamo liearni funkcional 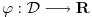 takav da za ma koje takav da za ma koje 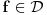 i niz i niz 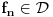 za koji je za koji je 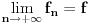 važi važi 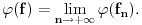 Skup svih distribucija obeležavamo sa Skup svih distribucija obeležavamo sa 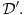 Ako je Ako je  distribucija, a distribucija, a  osnovna funkcija, umesto osnovna funkcija, umesto 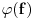 pisaćemo pisaćemo 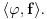 Preslikavanje koje svakoj osnovnoj funkciji pridružuje njenu vrednost u tački 0 ispunujava uslove iz definicije distribucije. Obeležavamo ga sa  i zovemo je Dirakovom distribucijom. Dakle, po definiciji Dirakove distribucije je i zovemo je Dirakovom distribucijom. Dakle, po definiciji Dirakove distribucije je 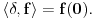 [ Nedeljko @ 15.05.2007. 16:47 ] @
Ako je
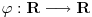 lokalno integrabilna funkcija (što znači da na svakom ograničenom intervalu ima smisla govoriti o njenom integralu), onda se odgovarajuća distribucija obeležava istim simbolom i definiše sa lokalno integrabilna funkcija (što znači da na svakom ograničenom intervalu ima smisla govoriti o njenom integralu), onda se odgovarajuća distribucija obeležava istim simbolom i definiše sa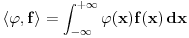 To je uvek distribucija i distribucije koje opisanim postupkom nastaju od obi;nih lokalno integrabilnih funkcija yovemo regularnim ditribucijama. Sve ostale distribucije zovemo singularnim. Dirakova distribucija je primer singularne distribucije. Sa druge strane, izvod To je uvek distribucija i distribucije koje opisanim postupkom nastaju od obi;nih lokalno integrabilnih funkcija yovemo regularnim ditribucijama. Sve ostale distribucije zovemo singularnim. Dirakova distribucija je primer singularne distribucije. Sa druge strane, izvod 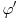 proizvoljne distribucije proizvoljne distribucije  (regularne ili singularne) se definiše jednakošću (regularne ili singularne) se definiše jednakošću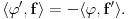 Najzad, da izračunamo izvod Hevisajdove distibucije H. Za proizvoljno 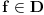 važi važi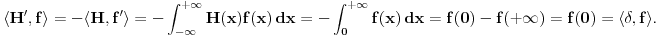 Pošto ovo važi za svako 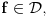 sledi da je sledi da je 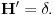 [ petarm @ 20.05.2007. 16:37 ] @
Mislim da je ovo i istorijski veoma zanimljivo. Naime Dirak je napisao "Metode kvantne fizike" gde je pomocu delta fje uradio sva izvodjenja i dobio rezultate. Kasnije je Neumann sve ovo egzaktno izveo matematicki primenom mera i to napisao u delu "Matematicke metode kvantne fizike", ali je dobio rezultate koji su se poklapali sa Dirakovim :) Te nije oborio Dirakovu teoriju vec joj je samo pomogao da stane na noge!
[ petarm @ 15.07.2007. 20:00 ] @
Imam pitanja. Naime receno je gore da je delta fja linearan operator, ali takodje i da je distribucija. Da li je pravilno reci da je nesto i operator i distribucija? To me malo zbunjuje. I da li je pravilno reci da je delta fja prosirenje Kronekerovog delta simbola na kontinuum? Zaista bih voleo da neko odgovori na ova pitanja! I zaista me buni kad neko kaze "dovoljno" glatka fja ili "dovoljno" lepa fja ili sl
[ tomkeus @ 16.07.2007. 00:55 ] @
Citat: petarm: Imam pitanja. Naime receno je gore da je delta fja linearan operator, ali takodje i da je distribucija. Da li je pravilno reci da je nesto i operator i distribucija? To me malo zbunjuje. I da li je pravilno reci da je delta fja prosirenje Kronekerovog delta simbola na kontinuum? Zaista bih voleo da neko odgovori na ova pitanja! I zaista me buni kad neko kaze "dovoljno" glatka fja ili "dovoljno" lepa fja ili sl :) Sta znaci to "dovoljno" i koliko je to "dovoljno"? Unapred hvala na odgovoru! Ja se nadam da ovde nisu pomešao pojam distribucije u statističkom smislu i pojam distrubucije u funkcionalnoj analizi. Delta funkcija je ovo drugo. Inače u prostor distribucija 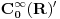 u funkcionalnoj analizi se definiše kao skup linearnih funkcionala (odatle operatorski deo) koji deluju na prostor u funkcionalnoj analizi se definiše kao skup linearnih funkcionala (odatle operatorski deo) koji deluju na prostor 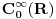 , tj. prostor svih beskonačno diferencijabilnih funkcija koje su van nekog konačnog intervala jednake nuli. Dakle distribucija , tj. prostor svih beskonačno diferencijabilnih funkcija koje su van nekog konačnog intervala jednake nuli. Dakle distribucija 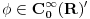 je preslikavanje je preslikavanje 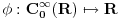 koje je pri tome linearno tj. za koje je pri tome linearno tj. za 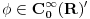 i i 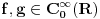 važi važi 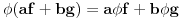 gde su a i b konstante . Pri tome su distribucije neprekidne u odnosu na Švarcovu konvergenciju u gde su a i b konstante . Pri tome su distribucije neprekidne u odnosu na Švarcovu konvergenciju u 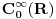 , tj za niz funkcija , tj za niz funkcija 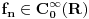 koji konvegira u Švarcovom smislu ka funkciji koji konvegira u Švarcovom smislu ka funkciji 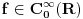 važi da važi da 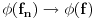 (ovo je ono što je Nedeljko napisao samo na malo fizičarskiji način). (ovo je ono što je Nedeljko napisao samo na malo fizičarskiji način).Prostor svih beskonačno diferencijabilnih funkcija koje su van nekog konačnog intervala jednake nuli je uzet upravo zbog svojstva "dovoljne glatkosti". Matematičarima to nije bitno i njima su daleko interesantniji funkcionalni prostori koji nisu tako "pitomi". Međutim, pošto je analiza osnovno matematičko oruđe kojim se služe fizičari, njima je potrebno da funkcije uvek mogu da se diferenciraju, integrale, razvijaju u redove itd. do mile volje. Srećna okolnost (možda je ovde bolje upotrebiti reč "nužnost") je da se priroda zapravo i ponaša na "gladak" način, tj. malom uzroku odgovaraju i male posledice (u malim vremenskim intervalima) tako da su u osnovi funkcije kojima opisujemo prirodu glatke. Usput je ubačen i zahtev da funkcije budu nenulte samo unutar nekog konačnog intervala što odgovara prirodi jer su u osnovi svi sistemi kojima se bavimo lokalizovani u konačnom delu prostora (ma koliko veliki on bio) [Ovu poruku je menjao tomkeus dana 16.07.2007. u 10:46 GMT+1] [ petarm @ 16.07.2007. 01:57 ] @
Ja bih ustvari distribucije u smislu funkcionalne analize mogao definisati kao granice neprekidnih fja. Zar ne?
[ tomkeus @ 16.07.2007. 10:49 ] @
[ tomkeus @ 16.07.2007. 13:47 ] @
Citat: petarm: I da li je pravilno reci da je delta fja prosirenje Kronekerovog delta simbola na kontinuum? U rigoroznom matematičkom smislu: Nemam pojma, zato što ne znam kako matematičari definišu "proširenje" Kronekereovog simbola na kontinuum, ako uopšte to i rade. U smislu analogija: Može se reći zato što ako integral posmatramo kao "kontinualnu sumu" delta funkcija se ponaša kao Kronekerov simbol zato što "ubija" sumu. Slikovitije: Ovako deluje Kronekerov simbol 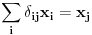 Ovako deluje delta funkcija 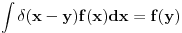 Kao što vidiš, upotreba je totalno analogna. [ petarm @ 16.07.2007. 21:16 ] @
Znam to. Dirakova delta fja i ima to delta u imenu od Kronekerovog delta simbola. Iz razloga koji si naveo. Pitanje ostaje i dalje da li delta fju mogu posmatrati kao prosirenje Kronekerovog delta simbola na kontinuum?
[ tomkeus @ 16.07.2007. 23:30 ] @
Citat: petarm: Znam to. Dirakova delta fja i ima to delta u imenu od Kronekerovog delta simbola. Iz razloga koji si naveo. Pitanje ostaje i dalje da li delta fju mogu posmatrati kao prosirenje Kronekerovog delta simbola na kontinuum? Već sam ti rekao:Opisno govoreći, ako sumu pretvorišu i untegral, a indekse u promenljive onda možeš. Ovde mi doduše nije skroz jasno šta podrazumevaš pod pojmom "proširenje" i zašto ti je to toliko bitno. [ petarm @ 17.07.2007. 10:13 ] @
"Prosirenje". Mislim da izraz "produzenje" ne bi bio dobar obzirom da bi moglo da se pobrka sa analitickim produzenjem a to shvakako ne bi bilo OK. Mozda ti se vise svidja ovako:Ako predjemo sa diskontinuuma na kontinuum da li Kronekerov delta simbol postaje Dirakova delta fja? Ja ipak mislim da je to vrlo vazno. Jer mi ovek u granicnim procesima tezimo da pravimo neke analogije ne bi li izveli neke zakljucke i dosli do odredjenog rezultata. Iako je priroda sama po sebi diskretna mi nekad tezimo da je posmatramo kao "razmazanu".
[ tomkeus @ 17.07.2007. 10:54 ] @
Citat: petarm: "Prosirenje". Mislim da izraz "produzenje" ne bi bio dobar obzirom da bi moglo da se pobrka sa analitickim produzenjem a to shvakako ne bi bilo OK. Mozda ti se vise svidja ovako:Ako predjemo sa diskontinuuma na kontinuum da li Kronekerov delta simbol postaje Dirakova delta fja? Ja ipak mislim da je to vrlo vazno. Jer mi ovek u granicnim procesima tezimo da pravimo neke analogije ne bi li izveli neke zakljucke i dosli do odredjenog rezultata. Iako je priroda sama po sebi diskretna mi nekad tezimo da je posmatramo kao "razmazanu". Mislim da sam konačno shvatio ono što hoćeš da pitaš: Recimo da je operacija "prelaska sa kontinuum na diskontinuum" dobro definisana matematička operacija predstavljena nekom funkcijom koja preslikava kontinualne skupove u odgovarajuće diskretne skupove, kontinualne strukture (operatori, funkcije itd.) u njima odgovarajuće diskretne strukture. Ono što tebe zanima (koliko sam shvatio) je da li postoji teorema koja kaže da će se pri dejstvu ove operacije delta funkcija preslikati u Kronekerovu deltu (takođe i obrnuto, tj. da li će se pri obrnutom postupku kronekerova delta preslikati u delta funkciju). Prilično sam siguran da takva teorema ne postoji. Ono u šta nisam siguran je da tako nešto nije moguće dokazati. Što se fizike tiče, već sam nekoliko puta ponovio da na nivou analogija delta funkcija jeste svojevrsni analogon kronekerovoj delti, ali ova analogija se realizuje samo matematički, tj. ova analogija potiče od ponašanja koje ova dva objekta imaju u sumama, ali kada je priroda u pitanju, delta funkcija ima neku direktnu interpretaciju u vidu nečeg što je vrlo lokalizovano tj. diskretno dok Kronekerova delta predstavlja samo algebarski konstrukt i ništa više. [ petarm @ 27.10.2007. 15:10 ] @
Na ovom delu Foruma je napisano kada fja trpi konacan skok njen izvod trpi beskonacan skok. Ipak ima li smisla pricati o tome kad nama iz diferencijabilnosti sledi neprekidnost? Odnosno izvod definisemo samo tamo gde je fja neprekidna.
[ reni90 @ 10.04.2011. 13:36 ] @
kako dirakova funkcija utice na pocetne uslove neke linearne dif, jednacine
naime nasao sam i u jednoj zbirci Sistemi Automatskog upravljanja od Kecman-a gdje kaze da ako imamo dif jednacinu n tog reda da je na ulazu dirakova impulsna funkcija onda mozemo rijesiti jednacinu tako sto je rijesavamo bez dirakove impulsne funkcije ali pocetne uvijete u 0+ izmijenimo zna li neko nesto vise o ovome trazio sam po netu nisam nista nasao u zbirci su samo date gotove opce formule sta se gdje uvrstava ali nije izvodjenje niti neko objasnjenje Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|