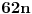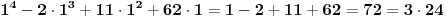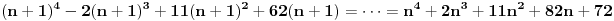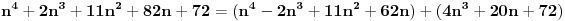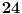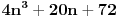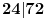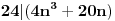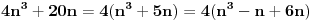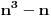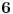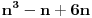[ ivanujcic @ 18.04.2007. 21:27 ] @
| Nasao sam ovaj zadatak u jednoj zbirci za 3.razred gimnazije i ne mogu da ga resim Dokazati da je n^4 - 2n^3 +11n^2 + 62 deljivo sa 24. Ja sam posao od ovoga: 24 sam razdvoio na 4 i 6. Broj je deljiv sa 6 kada je u obliku n^3-n ali nista nisam uspeo da uradim u vezi toga. Broj je deljiv sa 2 kada je u obliku n^2+n odnosno n^2-n. Veoma sam zainteresovan za ovaj zadatak. Radio sam ga 1.5h ali nista. Uostalom ja sam osmi razred osnovne skole ali mislim da to nije tesko uraditi, samo ima neka caka. [Ovu poruku je menjao ivanujcic dana 18.04.2007. u 23:09 GMT+1] |