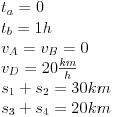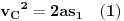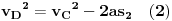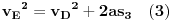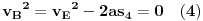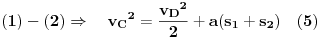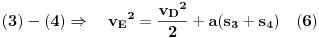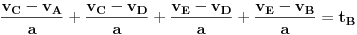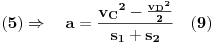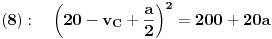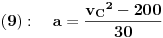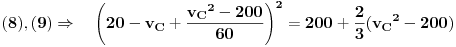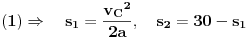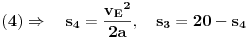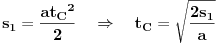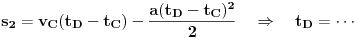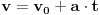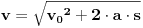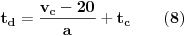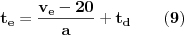[ Milan Milosevic @ 20.04.2007. 20:17 ] @
| Znam da ne volite puno da racunate ali nebi bilo lose da mi neko resi ovaj zadatak. Prosto sam se umorio od teorije pa da malo racunamo konkretne probleme. Zadatak glasi: Vi ste taksista koji vozi bolesnog putnika od mesta A do mesta B duz pravog puta.U trenutku polaska i kraja puta brzina taksija je nula.Rastojanje izmedu A i B je 50Km. Na rastojanju 30km od mesta A nalazi se most zanemarljive duzine sa ogranicenjem brzine od 20 km/h. Putnika treba prevesti za vreme ne duze od 1h. Sam bolesnik ima cudnu bolest tako da ne trpi inercijalnu silu. Naci zakon puta tako da u svakom trenutku putovanja putnik trpi minimalnu inercijalnu silu. |